β(ベータ)を理解する
【β(ベータ)を理解する】
CAPM(Capital Asset Pricing Model)は、「資本資産価格モデル」と訳される考え方です。
そしてCAPMを理解するためには、「β(ベータ)」を知ることが大変重要となります。
β(ベータ)とは、個別の株式の「リスク」を定量的に把握するための指標です。
ここではβ(ベータ)とは何かということ、またβ(ベータ)の特徴などについて学んでいきましょう。
【β(ベータ)とは】
上述したように、β(ベータ)とは個別の株式のリスクを定量的に把握するための指標です。
定量的にということなので、それは数値化されます。
具体的には、β(ベータ)の定義は以下のようになります。
「マーケットポートフォリオに対して、個別株式のリスクとリターンがどの程度大きいかを表した数値」
例えばリスク資産の運用で最強とされるマーケットポートフォリオの収益率が10%だった場合、または−10%だった場合などに、個別の株式がどれくらいの収益をあげることができるかを判断するための指標ということです。
【β(ベータ)の計算方法】
β(ベータ)を計算する際は、以下のような方法で行います。
なお、マーケットポートフォリオとして採用するポートフォリオには日経平均株価やTOPIXなどがありますが、ここではTOPIXをマーケットポートフォリオとして考えてみます。
TOPIXとは、東京証券取引所の第一部に上場している全ての会社の株式を対象として算出される株価指数です。
日経平均株価は会社が固定されているのに対して、TOPIXはすべての会社が対象となっていることが特徴となっています。
そして、β(ベータ)を計算したい会社をK社とします。
ここで、K社は株式市場に上場している会社であることが大前提です。
日々の株価の動きがわからなければ、β(ベータ)を計算することができないためです。
そしてTOPIXの収益率に対するK社のβ(ベータ)の値を計算していきます。
β(ベータ)の計算式は、以下の通りです。
β(ベータ) = (マーケットポートフォリオと個別株式の共分散)÷マーケットポートフォリオの分散
実務的にはβ(ベータ)は証券会社などが公表しているデータを使うことが一般的なので、ここでは計算式は「そういうもの」として考えておくだけで問題はありません。
そしてイメージとしては、以下のような図を用いると視覚的にわかりやすくなります。
例えばある日のTOPIXが10%上昇したとき、K社の株式が5%上昇した場合は、以下のように点を打ちます。
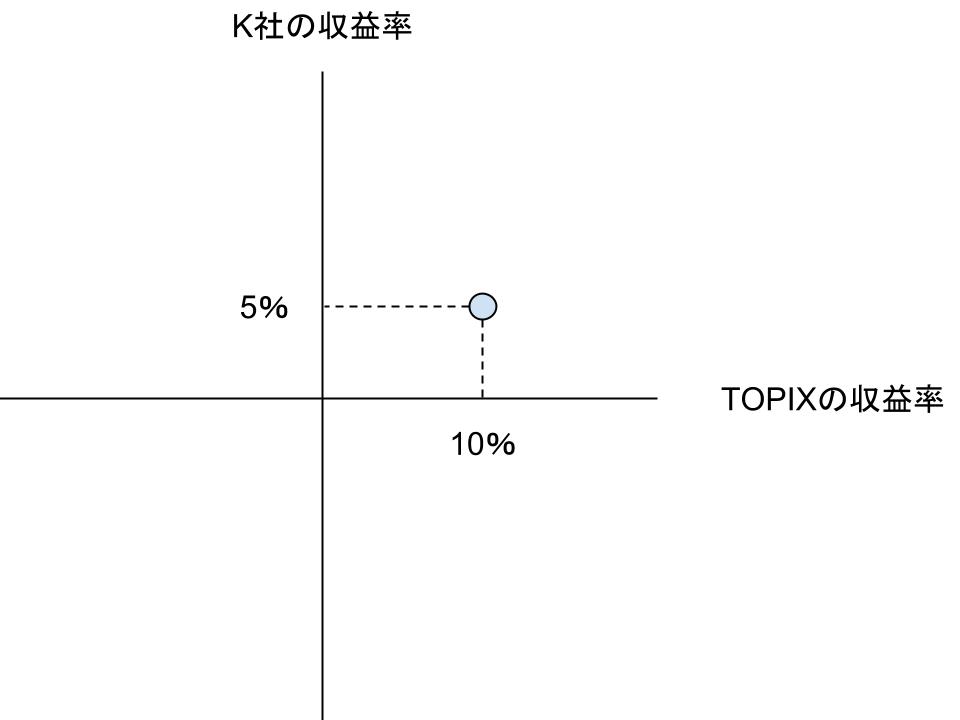
そしてその点と基準点を結んだ直線の傾きがβ(ベータ)です。
今回はわかりやすく下記の状況で考え、計算もしてみましょう。
今回のデータは以下です。
1年前を基準値とする(0)
↓
・現在のTOPIX 10%上昇
・現在のK社株 5%上昇
2年前を基準値とする(0)
↓
・1年前のTOPIX 5%上昇
・1年前のK社株 2.5%上昇
この例では簡単に考えているので、見ただけでK社の株式はTOPIXの半分の収益率になっているとわかります。
ではβ(ベータ)を計算してみましょう。
・期待収益率
TOPIX (10+5)÷2 = 7.5
K社株 (5+2.5)÷2 = 3.75
・TOPIXの偏差
1年前から現在 10−7.5 = 2.5
2年前から1年前 5−7.5 = −2.5
・K社株の偏差
1年前から現在 5−3.75 = 1.25
2年前から1年前 2.5−3.75 = −1.25
・TOPIXの分散
(2.52+(−2.5)2)÷2 = 6.25
・TOPIXとK社株の共分散
((2.5×1.25)+(−2.5)×(−1.25))÷2 = 3.125
β(ベータ)(TOPIXとK社の株式の共分散÷TOPIXの分散) = 3.125÷6.25 = 0.5
β(ベータ)は0.5です。
そしてこれを図示すると、以下のようになります。
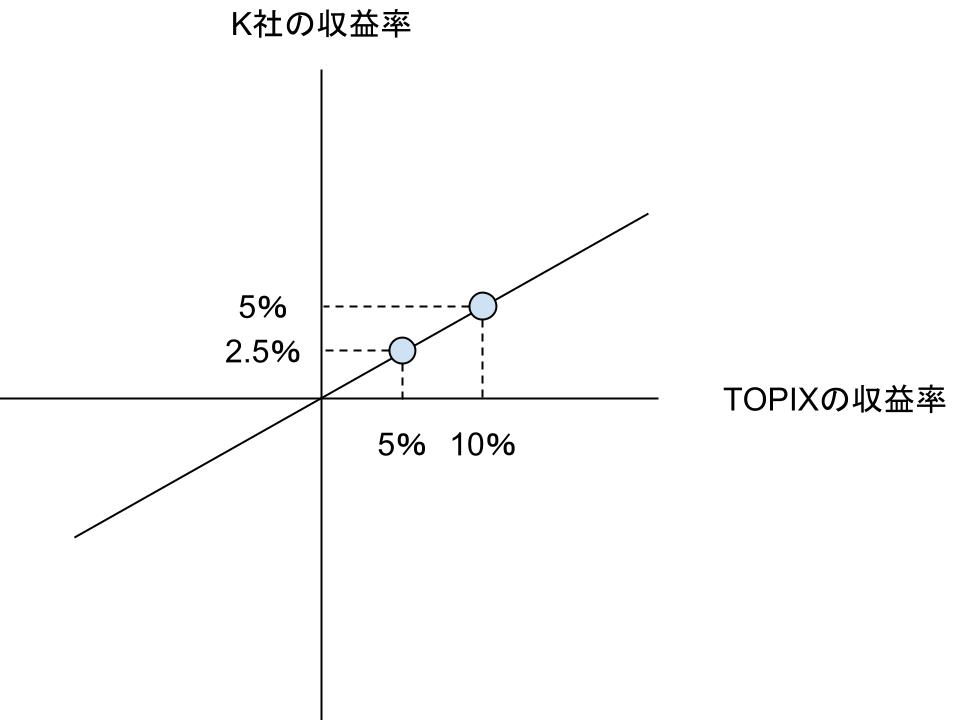
β(ベータ)が0.5のときは、傾きが45度の直線になっています。
そしてこれを様々なケースで考えると、β(ベータ)は以下のようになります。
≪マーケットポートフォリオの収益率が10%の場合≫
・個別株式の収益率が−20%だった → β(ベータ) = −2
・個別株式の収益率が−15%だった → β(ベータ) = −1.5
・個別株式の収益率が−10%だった → β(ベータ) = −1
・個別株式の収益率が−5%だった → β(ベータ) = −0.5
・個別株式の収益率が0%だった → β(ベータ) = 0
・個別株式の収益率が5%だった → β(ベータ) = 0.5
・個別株式の収益率が10%だった → β(ベータ) = 1
・個別株式の収益率が15%だった → β(ベータ) = 1.5
・個別株式の収益率が20%だった → β(ベータ) = 2
マーケットポートフォリオの収益率が10%のときに個別株式の収益率が10%だったとすると、β(ベータ)は1です。
逆に、個別株式の収益率が−10%だったとすると、β(ベータ)は−1です。
つまり、同じ動きをする場合は1、逆の動きをすると−1ということです。
これは相関に似ていますが、相関と異なるのは1以上、あるいは−1以下にもなるということです。
そして±1以上の場合はマーケットポートフォリオよりもハイリスクハイリターンであることを意味しています。
【β(ベータ)の傾向】
β(ベータ)は個別の株式のリスクとリターンを表す指標ですが、似た傾向を持つ会社は同じようなβ(ベータ)になることが多くなります。
同じようなβ(ベータ)の傾向が表れるのは、主に以下のような場合です。
≪業種が似ている場合≫
まず最も顕著に現れるのは、その業種です。
例えば景気によって業績が大きく変化する業種などは、β(ベータ)も大きくなる傾向にあると言えます。
具体的には、景気によって受注動向が左右されやすい紙や鉄鋼などの素材を扱う業種や建設業などです。
これに対して生活に密着した業種の会社などは常にある程度の需要が見込まれると考えられるため、β(ベータ)は小さくなります。
具体的には、食品や交通機関などです。
≪自己資本比率が似ている場合≫
次に、自己資本比率の割合も比較的β(ベータ)に影響を与えるとされています。
自己資本比率とは、総資本に占める自己資本の割合のことです。
例えば自己資本比率が高く負債が少ない場合は、多い場合と比べると、優先的に保護される債権者の割合が少ないということになるので、β(ベータ)は低い(リスクが低い)場合が多くなります。
同じ業種でも自己資本比率の違いによって、β(ベータ)は変わってくる場合があるということです。
【β(ベータ)参照時の注意点】
β(ベータ)はマーケットポートフォリオと個別株の関連性を示す非常に有用な指標です。
しかし注意点もあります。
それは、あくまでもβ(ベータ)は過去の数字であるということです。
例えば業種などで考えた場合、産業構造に変化がない場合は過去と未来でβ(ベータ)が大きく変わるということはありません。
しかし、会社の財務状況が変わることは比較的よくあることです。
これまで無借金経営を続け財務の安定性が高かった会社が、借り入れを積極的に行うなどの方針転換を行った場合などは、それまでよりもβ(ベータ)は高くなる可能性が高いということになります。
また、β(ベータ)はあくまでも株式を上場している会社で計算できる数値です。
上場していない会社の場合は投資家による自由な株式の売買が行われにくいため、計算することが難しくなります。
β(ベータ)は定量的に個別の会社のリスクを計算することが可能な指標ですが、上記のような注意点があることを頭に入れておきましょう。
関連ページ
- 運転資金を即日調達する方法「ファクタリング」とは?【Q&A付き】
- 財務諸表とファイナンス その1
- 財務諸表とファイナンス その2
- 資金計画を考える
- ファンダメンタル価値理論と砂上の楼閣理論
- 資金調達方法(負債と自己資本) その1
- 資金調達方法(負債と自己資本) その2
- 資金調達方法(負債と自己資本) その3
- NPVによる投資評価 その1
- NPVによる投資評価 その2
- IR(インベスター・リレーションズ)とは
- IRR(Internal Rate of Return:内部収益率)
- リースファクター(年金現価係数) その1
- リースファクター(年金現価係数) その2
- 負債を活用した場合のNPV
- M&A(企業の合併・買収) その1
- M&A(企業の合併・買収) その2
- 企業経営とキャッシュフロー概念 その1
- 企業経営とキャッシュフロー概念 その2
- MVA(Market Value Added:市場付加価値)
- NPVの注意点
- 資本コスト算定の注意点
- NPVとAPVの関係
- NPV(Net Present Value:正味現在価値)
- CAPMの公式と解明 その1
- CAPMの公式と解明 その2
- 最適資本構成とMM理論 その1
- 最適資本構成とMM理論 その2
- オプションを理解する その1
- オプションを理解する その2
- 永続価値を理解する その1
- 永続価値を理解する その2
- PI(Profitability Index:収益性指標)
- ポートフォリオの拡張と最適ポートフォリオ
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その1
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その2
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その3
- 現在価値を理解する その1
- 現在価値を理解する その2
- 現在価値の計算
- 利益還元政策を理解する その1
- 利益還元政策を理解する その2
- 「格付け」を理解する
- リアルオプションを理解する
- リスクとリターン その1
- リスクとリターン その2
- リスクとリターン その3
- リスクを理解する その1
- リスクを理解する その2
- リスクとポートフォリオ その1
- リスクとポートフォリオ その2
- 証券化とは
- ファイナンスのための統計学基礎
- 経営戦略とファイナンス その1
- 経営戦略とファイナンス その2
- 埋没コストと機会費用
- 株価の理論値を理解する その1
- 株価の理論値を理解する その2
- バリュエーションを理解する
- 資本コスト(WACC)を理解する その1
- 資本コスト(WACC)を理解する その2
- ブラック-ショールズの公式
- 回収期間(Payback)法と会計上の収益率 その1
- 回収期間(Payback)法と会計上の収益率 その2
- 株主に報いるには
- ファイナンスとは
- 「儲け」とは
- APV(Adjusted Present Value:調整現在価値)
- β(ベータ)を理解する
- CAPM(Capital Asset Pricing Model)とは
- キャッシュフローを理解する その1
- キャッシュフローを理解する その2
- キャッシュフローを理解する その3
- 連結決算が企業価値に与える影響
- コーポレートガバナンス(企業統治)を理解する その1
- コーポレートガバナンス(企業統治)を理解する その2
- 企業価値を理解する
- 負債コストとオプションの関係
- 経営の多角化が企業価値に与える影響
- 効率的市場仮説とランダムウォーク
- EVA(Economic Value Added:経済的付加価値)
- 財務レバレッジとβ(ベータ) その1
- 財務レバレッジとβ(ベータ) その2
- 財務レバレッジとβ(ベータ) その3
- 財務政策を理解する
