リースファクター（年金現価係数）その1

トップページ＞ファイナンス（財務）＞リースファクター（年金現価係数）その1

【リースファクター（年金現価係数）を理解する】
永続価値を利用した意思決定の一つに、例えば「条件が異なるリースで、その年間費用をどう比較するか」ということがあります。

まず、リースがどのようなものかを知っておきましょう。

リースとは、固定資産を会社が購入するのではなく、リース会社と契約を結ぶことでリース会社が購入した固定資産を貸してもらう取引のことです。

リースにはファンナンスリースやオペレーティングリースなどという種類があり、原則としてファンナンスリースはその資産を貸借対照表に載せる必要があるもので、オペレーティングリースはその必要がないものです。
（固定資産の金額や会社の規模などによって異なります。）

例えば車で考えてみましょう。

車は購入すると当然のことながら最初に購入費用がかかり、これを定率法や定額法などの方法で減価償却していきます。

この場合、最初に購入費用を準備しておかなければなりません。

しかしリースで導入する場合は、この購入費用は不要で、決められた一定のリース料をリース会社に支払っていくことになります。

契約期間などによって月々の支払額が決まるため、支出を平準化できるというわけです。

これがリースです。

しかし資産をリースで導入する際に候補がいくつかある場合、契約期間の違いなどがあるためにどのリースのコストが最も安いかはすぐにはわかりません。

例えば3年リースと5年リースを比較した場合、当たり前ですが3年リースは3年間しか資産を使用できず、5年リースの場合は5年間資産を使用できます。

よってそのような場合、どちらのリース費用が安いかの意思決定を現在価値の考え方を使って、以下のように行うとします。

1．リースにかかる費用総額を現在価値に割り引く。
2．それぞれの現在価値を使用期間で割り、リース費用の年額を計算する。

上記の方法は、未来の費用が現在価値に割り引かれているため、意思決定は適切に行えそうに見えます。

しかし実はこの方法は厳密には適切ではありません。

なぜでしょうか？

それは、2の「使用期間で割り」の部分にあります。

まず、3年と5年のリースを比較するために年額費用を計算するのは正しい判断です。

そして1で費用総額を現在価値に修正するのも正しい判断です。

しかし、使用期間は修正されていません。

その結果、費用総額の現在価値をただ使用年数で割っても、「修正されたもの÷修正されていないもの」ということになり、厳密な意味での正しい結果は導けないのです。

よってここでは、費用総額を現在価値に修正していることから、「使用期間も現在価値に割り引く」という作業を行って初めて、計算として適切なものになります。

ちょっとわかりにくいですが、5年間のリースは「5年間使用する」権利があり、3年間のリースは「3年間使用する」権利があります。

そして費用総額は、この「異なる2年分」は加味していない現在価値です。

よってこの異なる2年分を公平にするために、使用期間を現在価値に割り引く必要があるのです。

そしてこの「使用期間も現在価値に割り引く」という考え方が「リースファクター」という考え方です。

このリースファクターは、別の側面から見ると「年金現価係数」とも呼ばれます。

一般的な用語としては、年金現価係数のほうがよく知られています。

そして年金現価係数は、例えば以下の場合にも使用されます。

・利息のつく預金から、毎年一定額の金額を複数年引き落としたい場合、最初に必要となる元本の金額を計算する。

・複数年同じキャッシュフローが長期にわたって発生する事業の現在価値を求める。

よってここでは、まずはリースを例にとってリースファクターという概念を学び、それが年金現価係数と同じであるということを理解しましょう。

なお、実際のリースの経済性に関する評価はリースの種類（上述したファイナンスリース、オペレーションリースなど）が多岐にわたるため複雑で、かつ様々な考え方が存在します。

よって今回は、あくまでも現在価値、あるいは永続価値のを理解を深めるための一例と考えてください。

【現在価値を利用したリース選択の意思決定】
ではまず、自動車をリースする場合の以下の２つのケースを考えてみましょう。

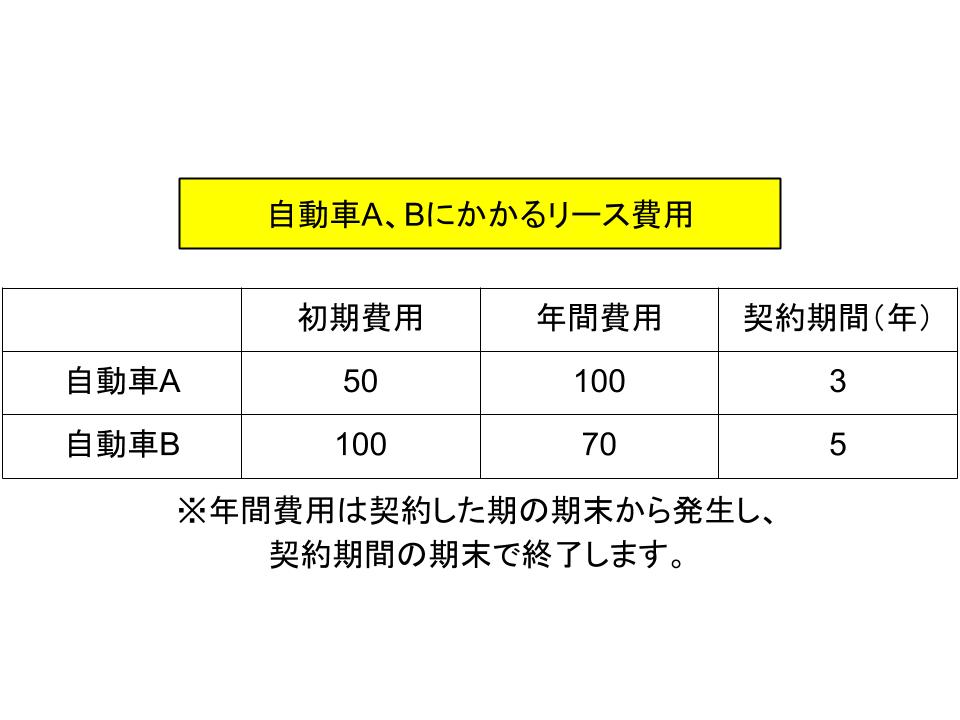
リースファクター（年金現価係数）

自動車Aは初期費用が安く年間費用は高いタイプで契約期間は3年、自動車Bは初期費用が高く年間費用が安いタイプで契約期間は5年です。

この2つの候補の費用総額の現在価値を求め、最終的に年間あたりの費用総額が安いほうを選択したいと考えています。

まずはこの自動車A、自動車Bそれぞれにかかる費用総額の現在価値を計算してみましょう。

なお、ここでは割引率を10％と考えています。

≪自動車A≫
PV　＝　50＋100÷（1.1）＋100÷（1.1）2＋100÷（1.1）3　≒　50＋90.91＋82.64＋75.13　＝　298.68　

≪自動車B≫
PV　＝　100＋70÷（1.1）＋70÷（1.1）2＋70÷（1.1）3＋70÷（1.1）4＋70÷（1.1）5　≒　　100＋63.64＋57.85＋52.59＋47.81＋43.46　＝　365.35

このようになり、費用総額の現在価値は自動車Bのほうが大きくなります。

これは自動車Bが2年契約期間が長いため、当然といえば当然です。

次に、いよいよ契約期間を現在価値に修正しましょう。

ここでは3年と5年という期間を、それぞれ現在価値に修正します。

これがリースファクター、あるいは年金現価係数と呼ばれるものです。

なお、この場合、発生するのはこれまで考えてきたキャッシュフローではなく、1年という期間です。

当然と言えば当然ですが、例えば1年後から2年後までの期間は1年ですし、4年後から5年後までの期間も1年です。

よってこれまで分子となっていたキャッシュフローは、すべて「1年間　＝　1」に置きかわります。

ではまず3年のリースファクター（年金現価係数）を計算してみましょう。

≪1年後から3年後の現在価値≫
PV　＝　1÷（1.1）＋1÷（1.1）2＋1÷（1.1）3　≒　0.9091＋0.8264＋0.7513　＝　2.4868

次に5年のリースファクター（年金現価係数）を計算してみましょう。

≪1年後から5年後の現在価値≫
PV　＝　1÷（1.1）＋1÷（1.1）2＋1÷（1.1）3＋1÷（1.1）4＋1÷（1.1）5　≒　00.9091＋0.8264＋0.7513＋0.6830＋0.6209　＝　3.7907

これでそれぞれの期間の現在価値がわかりました。

そして最終的なリース費用の年額を計算するために、先ほど計算したリース費用総額の現在価値を3年と5年の現在価値で割ります。

≪自動車Aのリース費用（年額）≫
リース費用（年）　＝　298.68÷2.4868　≒　120.11

≪自動車Bのリース費用（年額）≫
リース費用（年）　＝　365.35÷3.7907　≒　96.38

自動車Aのリース費用／年が120.11、自動車Bのリース費用／年が96.38です。

これで自動車Bのリース費用が安いとわかりました。

ファイナンス的に行った意思決定は、「自動車Bをリースする」です。

次のページ　「リースファクター（年金現価係数）その2」

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど