ポートフォリオの拡張と最適ポートフォリオ
【ポートフォリオの拡張と最適ポートフォリオ】
前回は個別資産のリスクとリターン、ポートフォリオを組んだ時のリスクとリターンについて学びました。
今回は、そのポートフォリオを別の視点から拡張し、「最適なポートフォリオ」について考えてみましょう。
【ポートフォリオの拡張】
まずはポートフォリオの種類を拡大してリスクフリーな金融商品を組み込み、リスクとリターンを考えてみます。
今回は、輸出関連企業であるO社の株式と、金利が2%の国債でポートフォリオを組んでみます。
・O社
期待収益率:6%
円高の場合の偏差:−16
円安の場合の偏差:14
不変の場合の偏差:−6
分散:144
標準偏差:12
・金利が2%の国債
期待収益率:2%
円高の場合の偏差:0
円安の場合の偏差:0
不変の場合の偏差:0
分散:0
標準偏差:0
そして今回も、O社と国債に50%ずつ投資するとして考えてみましょう。
念のため、前提条件を振り返っておきます。
・今後の為替レート予想
今後円高になる確率:20%
今後円安になる確率:40%
今後不変である確率:40%
・O社の収益率の変化
円高:収益が10%ダウン
円安:収益が20%アップ
不変:収益に影響はない
そして具体的に計算してみると、以下のようになります。
≪期待収益率≫
・円高の場合
・O社への投資分(50%)の期待収益率 −10%×0.5 = −5%
・国債への投資分(50%)の期待収益率 2%×0.5 = 1%
・O社、国債への投資合計 −5%+1% = −4%
・円安の場合
・O社への投資分(50%)の期待収益率 20%×0.5 = 10%
・国債への投資分(50%)の期待収益率 2%×0.5 = 1%
・O社、国債への投資合計 10%+1% = 11%
・不変の場合
・O社への投資分(50%)の期待収益率 0%×0.5 = 0%
・国債への投資分(50%)の期待収益率 2%×0.5 = 1%
・O社、国債への投資合計 0%+1% = 1%
・O社、国債に50%ずつ投資した場合の期待収益率
−4%×0.2+11%×0.4+1%×0.4 = −0.8+4.4+0.4 = 4%
≪偏差≫
円高:(−4)−4 = −8
円安:11−4 = 7
不変:1−4 = −3
≪分散≫
((−8)2×0.2)+(72×0.4)+((−3)2×0.4) = 12.8+19.6+3.6 = 36
≪標準偏差≫
√36 = 6
そして前回同様、これを割合を変えて計算してみると、以下のようになります。
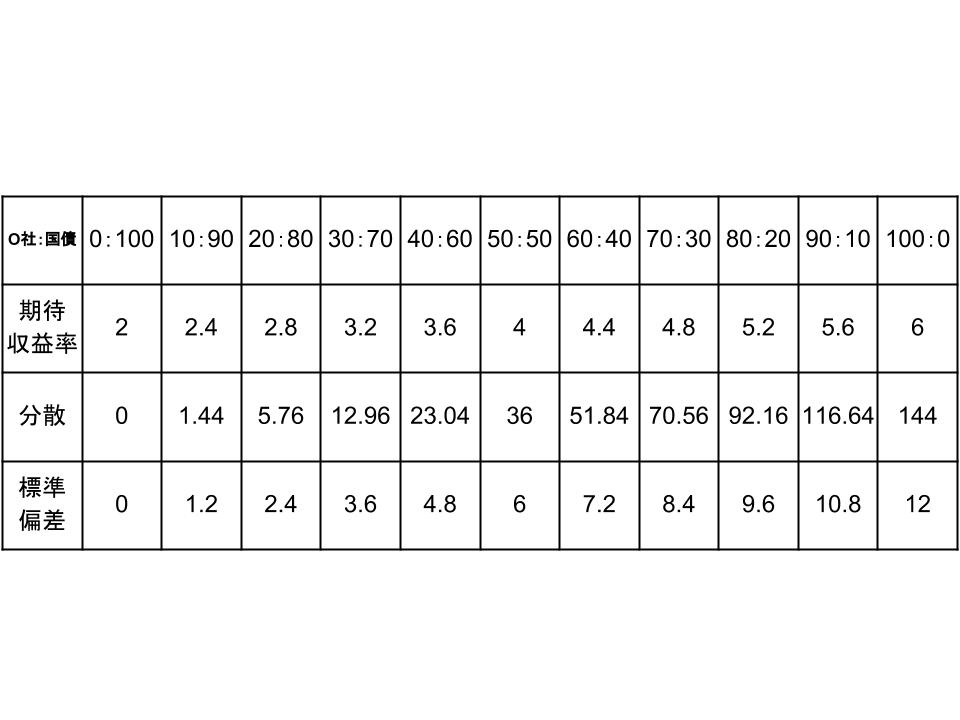
そして前回と同じく、図示してみます。
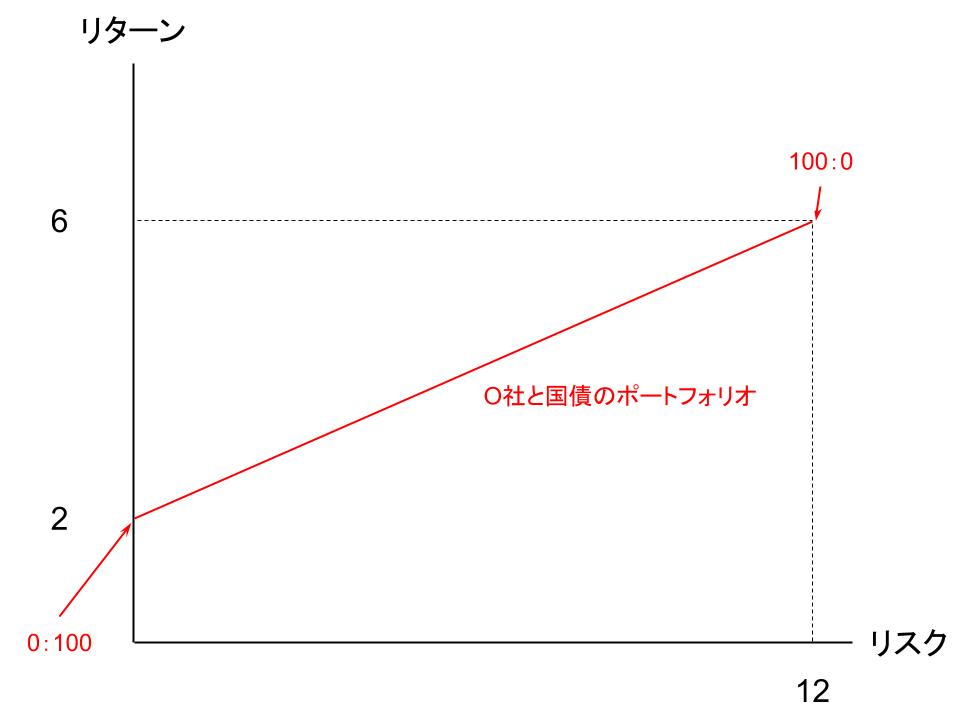
すると、今回は直線になることがわかります。
リスクのない国債をポートフォリオに組み入れると、そのリスクとリターンは直線になって表示されるということです。
これは、共分散と相関を考えてみてもわかります。
≪共分散≫
円高:(−16)×0 = 0
円安:14×0 = 0
不変:(−6)×0 = 0
0×0.2+0×0.4+0×0.4 = 0 = 0
≪相関≫
0÷(12×0) = 0
O社と国債の相関が「0」ということになり、データは関連なく動くということになります。
しかしこの場合は、国債は「もともと動かない」ために相関がない、つまりO社の動きだけにポートフォリオは左右されるということになっています。
そしてこの直線は、「資本市場線」と呼ばれます。
O社のようなリスク資産と国債のようなリスクフリーの資産を組み合わせたポートフォリオは、必ず直線になるということです。
また、今回はO社と国債のポートフォリオですが、これをO社と輸入関連企業であるP社のポートフォリオの中に図示してみます。
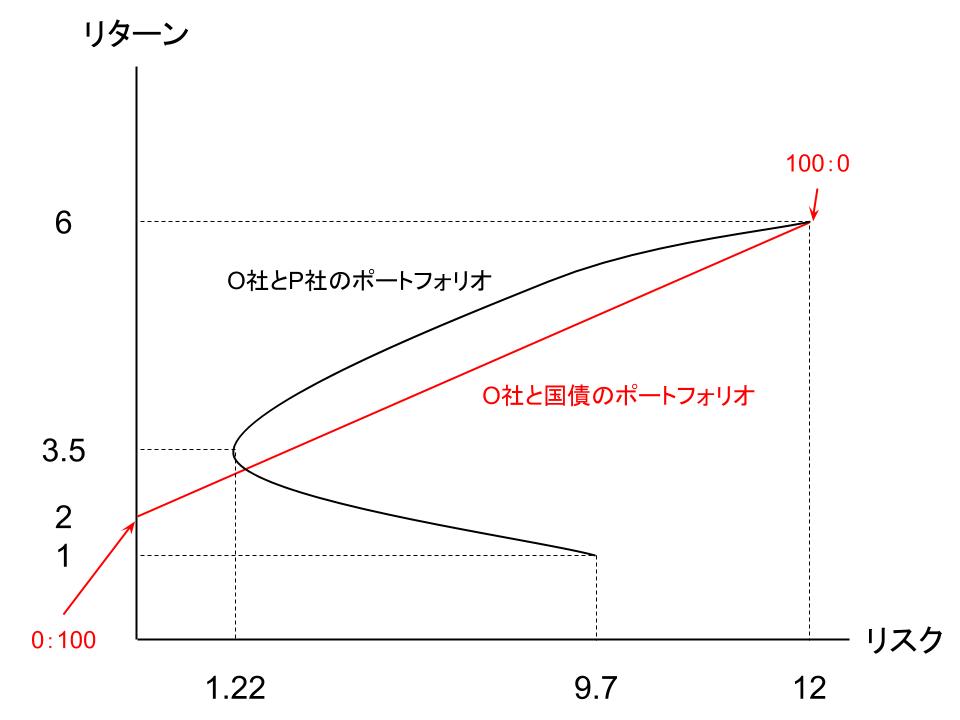
O社と国債の組み合わせは、O社と相関の高い(逆の動きをする)P社が入っていない分、リスクに見合うリターンを得ることができていないことがわかります。
そこで、最もリスクに対する期待収益率が高い、O社とP社の組み入れ比率が50:50のポートフォリオと国債を組み合わせてみることにします。
そしてまた割合を変えて計算してみると、以下のようになります。
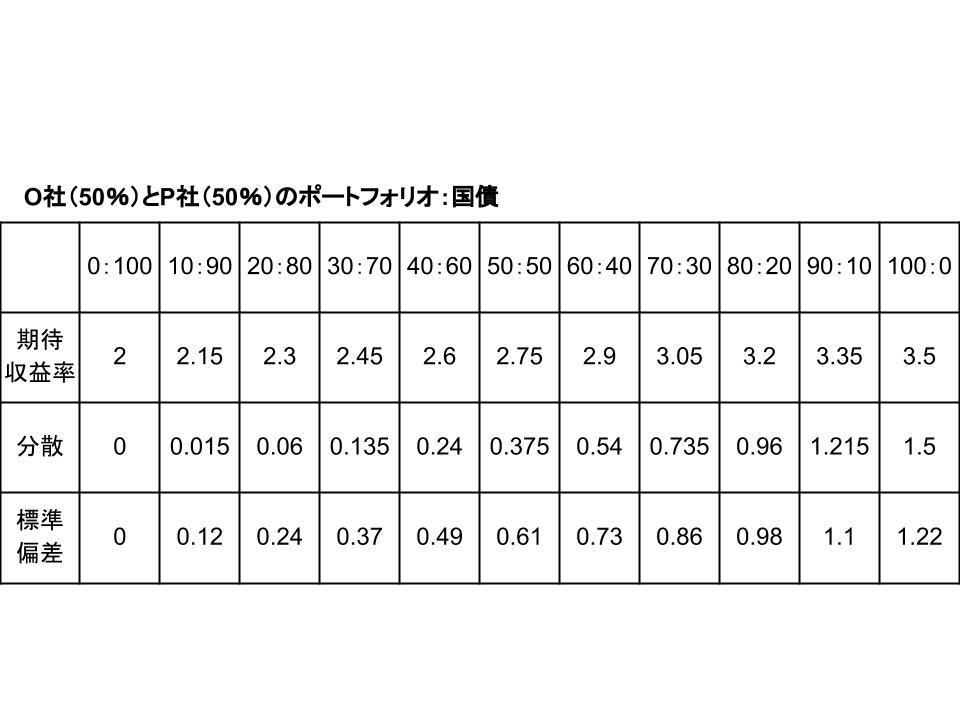
そして前回と同じく、図示してみます。
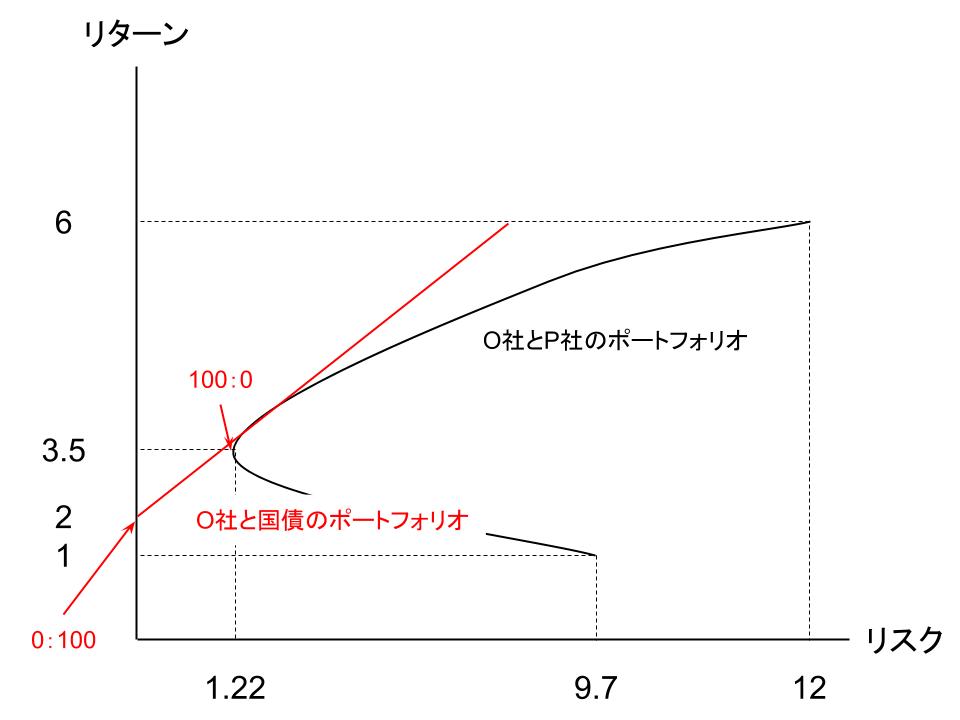
今度は直線の傾きが変わり、直線はO社とP社を50:50で組み入れたポートフォリオに向かって伸びています。
資本市場線のリスクに対する収益率が高まっているということです。
なお、この市場資本線の傾きはシャープレシオと呼ばれます。
シャープレシオは「(期待収益率−リスクフリーレート)÷リスク(標準偏差)」で計算することができます。
リスクフリーレートとはリスクフリーの資産の利回り、つまりここでは国債の利回りである2%です。
そしてこのシャープレシオが最大になる点が、直線と曲線の接点ということになり、最も効果的に収益をあげることのできるポイントとなります。
なお、今回の場合はO社とP社の組み入れ比率が50:50の場合と40:60の場合では、どちらが収益率が高いか直感的には判断しにくくなっていますので、シャープレシオで確認してみましょう。
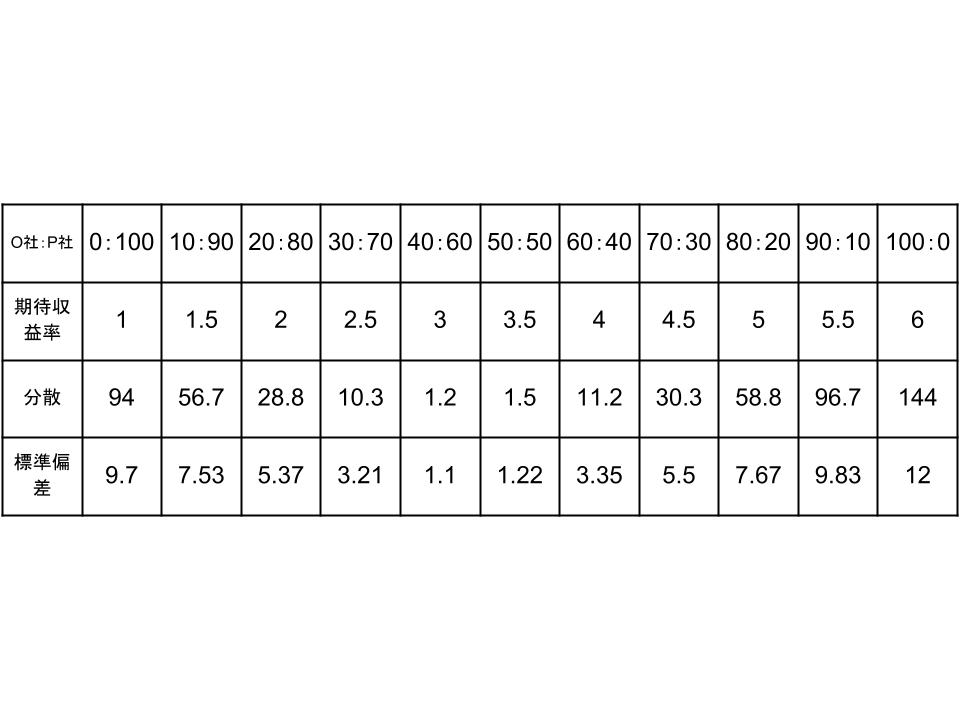
・O社とP社の組み入れ比率が50:50の場合のシャープレシオ
(3.5−2)÷1.22 ≒ 1.23
・O社とP社の組み入れ比率が40:60の場合のシャープレシオ
(3−2)÷1.1 ≒ 0.91
O社とP社の組み入れ比率が50:50の場合のほうが高くなっています。
なお、念のためにもう少しシャープレシオを計算してみましょう。
効率的フロンティアにあるO社とP社の組み入れ比率が60:40の場合のシャープレシオも計算してみます。
・O社とP社の組み入れ比率が60:40の場合のシャープレシオ
(4−2)÷3.35 ≒ 0.60
やはりO社とP社の組み入れ比率が50:50の場合が最もシャープレシオが高く、リスクに対するリターンが高いことがわかります。
【最適なポートフォリオとは】
ではここで、最適なポートフォリオとは何かについて考えてみましょう。
まず株式のようなリスク資産で組むポートフォリオでは、「効率的フロンティア」と呼ばれる曲線がリスクに対するリターンが高いポイントとなっていました。
そしてリスクフリーである国債などを追加した場合は、直線となる資本市場線が効率的フロンティアに接するようにポートフォリオを組んだ場合にそのリターンが最も高くなります。
よって、最適なポートフォリオとは、「リスク資産で組んだポートフォリオの効率的フロンティアに接するようにリスクフリーの資産を組み入れたポートフォリオ」となります。
そしてあとは「リスクフリーの資産をどの程度組み入れるか」によってそのリスクが変わってくるということです。
投資家のリスク許容度によってこの資本市場線上でポートフォリオが組まれるようになるのです。
なお、リスク資産だけで構成されるポートフォリオと資本市場線の接点は、マーケットポートフォリオと呼ばれます。
そして株式の場合のマーケットポートフォリオは、「すべての銘柄を持つ」ということです。
例えば今回はO社とP社でポートフォリオを組み、このポートフォリオには大きなリスク分散の効果がありました。
しかし、2社だけでは個別に発生するリスクを完全に抑えることはできません。
O社で何か不祥事などがあった場合は、その割合が高い分一気にリスクが高まることになります。
そして他の会社で株価を押し上げる何らかの大きな要素が発生した場合に、そのリターンを得ることもできません。
このような可能性を突き詰めていき、さらにマーケットリスク以外のリスクを最小限に抑えようとすると、必然的にすべての会社の株式を保有することが最適解となるのです。
ここでは、ポートフォリオは効率的フロンティアに接する「資本市場線」上以外で組まれることはなく、その中でリスク許容度によってリスクフリーの資産配分が決まるということを理解しておきましょう。
関連ページ
- 運転資金を即日調達する方法「ファクタリング」とは?【Q&A付き】
- 財務諸表とファイナンス その1
- 財務諸表とファイナンス その2
- 資金計画を考える
- ファンダメンタル価値理論と砂上の楼閣理論
- 資金調達方法(負債と自己資本) その1
- 資金調達方法(負債と自己資本) その2
- 資金調達方法(負債と自己資本) その3
- NPVによる投資評価 その1
- NPVによる投資評価 その2
- IR(インベスター・リレーションズ)とは
- IRR(Internal Rate of Return:内部収益率)
- リースファクター(年金現価係数) その1
- リースファクター(年金現価係数) その2
- 負債を活用した場合のNPV
- M&A(企業の合併・買収) その1
- M&A(企業の合併・買収) その2
- 企業経営とキャッシュフロー概念 その1
- 企業経営とキャッシュフロー概念 その2
- MVA(Market Value Added:市場付加価値)
- NPVの注意点
- 資本コスト算定の注意点
- NPVとAPVの関係
- NPV(Net Present Value:正味現在価値)
- CAPMの公式と解明 その1
- CAPMの公式と解明 その2
- 最適資本構成とMM理論 その1
- 最適資本構成とMM理論 その2
- オプションを理解する その1
- オプションを理解する その2
- 永続価値を理解する その1
- 永続価値を理解する その2
- PI(Profitability Index:収益性指標)
- ポートフォリオの拡張と最適ポートフォリオ
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その1
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その2
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その3
- 現在価値を理解する その1
- 現在価値を理解する その2
- 現在価値の計算
- 利益還元政策を理解する その1
- 利益還元政策を理解する その2
- 「格付け」を理解する
- リアルオプションを理解する
- リスクとリターン その1
- リスクとリターン その2
- リスクとリターン その3
- リスクを理解する その1
- リスクを理解する その2
- リスクとポートフォリオ その1
- リスクとポートフォリオ その2
- 証券化とは
- ファイナンスのための統計学基礎
- 経営戦略とファイナンス その1
- 経営戦略とファイナンス その2
- 埋没コストと機会費用
- 株価の理論値を理解する その1
- 株価の理論値を理解する その2
- バリュエーションを理解する
- 資本コスト(WACC)を理解する その1
- 資本コスト(WACC)を理解する その2
- ブラック-ショールズの公式
- 回収期間(Payback)法と会計上の収益率 その1
- 回収期間(Payback)法と会計上の収益率 その2
- 株主に報いるには
- ファイナンスとは
- 「儲け」とは
- APV(Adjusted Present Value:調整現在価値)
- β(ベータ)を理解する
- CAPM(Capital Asset Pricing Model)とは
- キャッシュフローを理解する その1
- キャッシュフローを理解する その2
- キャッシュフローを理解する その3
- 連結決算が企業価値に与える影響
- コーポレートガバナンス(企業統治)を理解する その1
- コーポレートガバナンス(企業統治)を理解する その2
- 企業価値を理解する
- 負債コストとオプションの関係
- 経営の多角化が企業価値に与える影響
- 効率的市場仮説とランダムウォーク
- EVA(Economic Value Added:経済的付加価値)
- 財務レバレッジとβ(ベータ) その1
- 財務レバレッジとβ(ベータ) その2
- 財務レバレッジとβ(ベータ) その3
- 財務政策を理解する
