現在価値を理解する その1
【現在価値を理解する】
これまで、ファイナンスを考えたときにまずはキャッシュフローを考えようということを学びました。
収益性を現金ベースで考えるということが、実際の経営には不可欠だからです。
そしてキャッシュフローとともに重要な考え方が、「現在価値」という考え方です。
会社を経営していくとき、常に必要なことは「未来の収益をどう把握するか」ということです。
未来の収益については、例えば新事業の候補がいくつかあった場合、その収益がいつ発生するか、どのくらい発生するかは各事業によって異なります。
そして仮にそれらの候補の中から1つを選択しなければいけない場合、それらのばらばらの期間に発生するばらばらの金額の収益を、ある基準によって統一して最も会社の利益となる事業を選択しなければなりません。
そのための基準として最適なのが、「現在価値」で考えるということです。
ここではまず現在価値が何かを知り、どのように使うべきなのかを学びましょう。
【金銭の時間的価値】
まず現在価値を考える前に、金銭には時間的価値があるということを学びましょう。
わかりやすく、2つの例で考えてみます。
≪例1≫
例えばYさんという人が宝くじに当たり、100万円もらえることになったとします。
そしてその宝くじには2つのオプションがあります。
オプション1
100万円を今すぐもらえる。
オプション2
100万円を5年後にもらえる。
Yさんはどちらのオプションを選択するのが正解でしょうか?
これを考える際は、まずYさんの事情を考慮する必要があります。
例えばYさんは5年後に100万円を支払う義務を負っており、かつ浪費癖があるので、今もらっても5年後にその金銭が残っている保証がないなどという場合は、オプション2を選択することが正解です。
万が一のために今はもらわずに、確実に5年後に返済できる担保として100万円をとっておくのです。
そうすれば、少なくとも5年後の返済に困ることはありません。
しかし、ファイナンス的に考えると、この選択は不正解です。
なぜなら、オプション1を選択して今金銭をもらえば、その金銭を何らかの形で投資することで、今の100万円が5年後には増えている可能性が高いためです。
これをもっともリスクの少ないと考えられる定期預金で考えてみましょう。
仮に定期預金の金利(複利)を5%とすると、100万円は5年後には以下のようになります。
(数値の開きがわかりやすいように、ここでは5%に設定しています。)
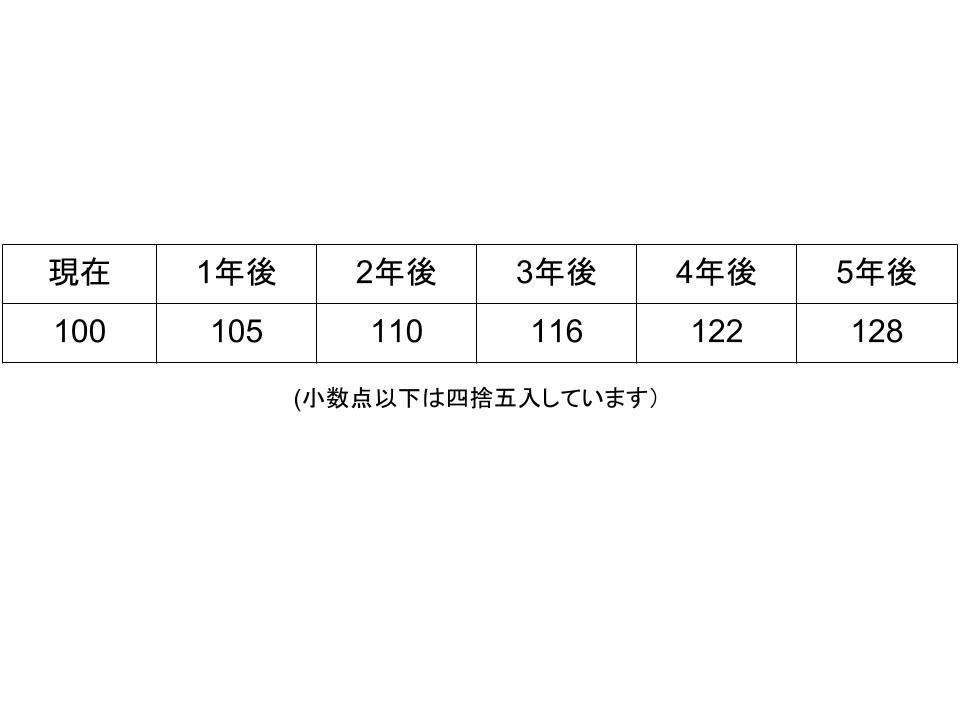
現在100万円だった金銭が、5年後には128万円になっているのです。
単純に考えると、オプション1とオプション2には、28万円の違いがあるということになります。
そして、この差が「金銭の時間的価値」と呼ばれるものです。
ここでは、「今もらう」ほうが得をするということになります。
≪例2≫
次に、使う場合を考えてみましょう。
今度はYさんが車を修理したとしましょう。
Yさんは修理を依頼している修理工場とは長い付き合いがあり、信頼関係もあります。
よってYさんがこの修理工場に修理を依頼する場合は、その支払いを以下から選択することができます。
オプション1
修理代金を今すぐ支払う。
オプション2
修理代金を半年後に支払う。
この場合はどちらのオプションを選択するのが正解でしょうか?
今度はYさんの個人的事情は考えず、ファイナンス的に考えてみましょう。
そうすると、正解はオプション2を選択することになります。
修理代金をすぐに支払わず、半年満期の定期預金などに入れておいてそれを解約してから支払えば、今すぐ支払うよりもその利息分を手にすることができるからです。
ここでは、「後で支払う」ほうが得をするということになります。
このように、金銭はもらう時間あるいは支払う時間によってその価値が異なります。
そして、金銭の時間的価値は、常に「今の金銭が未来の金銭よりも高い」という性質を持っています。
そのために例1の「もらう」ケースでは今のほうがよく、例2の「支払う」ケースでは後のほうがよいのです。
このことは、ローンなどを組んだ場合に必ず利息がつくことからもわかります。
未来に行くほど金銭の価値は下がるので、利息を追加しなければならないのです。
あるいは、保険料などで「一括払い」を選択すると割引が適用されるのもこの時間的価値が関係しています。
「最初に一気に支払う = 価値の高い金銭を支払う」ということになるので、割引が適用されるのです。
まずは「金銭には時間によって価値が異なる」ことを理解しましょう。
関連ページ
- 運転資金を即日調達する方法「ファクタリング」とは?【Q&A付き】
- 財務諸表とファイナンス その1
- 財務諸表とファイナンス その2
- 資金計画を考える
- ファンダメンタル価値理論と砂上の楼閣理論
- 資金調達方法(負債と自己資本) その1
- 資金調達方法(負債と自己資本) その2
- 資金調達方法(負債と自己資本) その3
- NPVによる投資評価 その1
- NPVによる投資評価 その2
- IR(インベスター・リレーションズ)とは
- IRR(Internal Rate of Return:内部収益率)
- リースファクター(年金現価係数) その1
- リースファクター(年金現価係数) その2
- 負債を活用した場合のNPV
- M&A(企業の合併・買収) その1
- M&A(企業の合併・買収) その2
- 企業経営とキャッシュフロー概念 その1
- 企業経営とキャッシュフロー概念 その2
- MVA(Market Value Added:市場付加価値)
- NPVの注意点
- 資本コスト算定の注意点
- NPVとAPVの関係
- NPV(Net Present Value:正味現在価値)
- CAPMの公式と解明 その1
- CAPMの公式と解明 その2
- 最適資本構成とMM理論 その1
- 最適資本構成とMM理論 その2
- オプションを理解する その1
- オプションを理解する その2
- 永続価値を理解する その1
- 永続価値を理解する その2
- PI(Profitability Index:収益性指標)
- ポートフォリオの拡張と最適ポートフォリオ
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その1
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その2
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その3
- 現在価値を理解する その1
- 現在価値を理解する その2
- 現在価値の計算
- 利益還元政策を理解する その1
- 利益還元政策を理解する その2
- 「格付け」を理解する
- リアルオプションを理解する
- リスクとリターン その1
- リスクとリターン その2
- リスクとリターン その3
- リスクを理解する その1
- リスクを理解する その2
- リスクとポートフォリオ その1
- リスクとポートフォリオ その2
- 証券化とは
- ファイナンスのための統計学基礎
- 経営戦略とファイナンス その1
- 経営戦略とファイナンス その2
- 埋没コストと機会費用
- 株価の理論値を理解する その1
- 株価の理論値を理解する その2
- バリュエーションを理解する
- 資本コスト(WACC)を理解する その1
- 資本コスト(WACC)を理解する その2
- ブラック-ショールズの公式
- 回収期間(Payback)法と会計上の収益率 その1
- 回収期間(Payback)法と会計上の収益率 その2
- 株主に報いるには
- ファイナンスとは
- 「儲け」とは
- APV(Adjusted Present Value:調整現在価値)
- β(ベータ)を理解する
- CAPM(Capital Asset Pricing Model)とは
- キャッシュフローを理解する その1
- キャッシュフローを理解する その2
- キャッシュフローを理解する その3
- 連結決算が企業価値に与える影響
- コーポレートガバナンス(企業統治)を理解する その1
- コーポレートガバナンス(企業統治)を理解する その2
- 企業価値を理解する
- 負債コストとオプションの関係
- 経営の多角化が企業価値に与える影響
- 効率的市場仮説とランダムウォーク
- EVA(Economic Value Added:経済的付加価値)
- 財務レバレッジとβ(ベータ) その1
- 財務レバレッジとβ(ベータ) その2
- 財務レバレッジとβ(ベータ) その3
- 財務政策を理解する
