ファイナンスのための統計学基礎
【ファイナンスのための統計学基礎】
ファイナンスでそのリスクとリターンを考える際、どうしても避けて通れないのが、統計に関する知識です。
ファイナンスのリスクとリターンは、その「数値」を根拠とするために、数値を算出するための基本的な統計の計算が必須になるためです。
よってここでは、リスクとリターンを考える前に、最低限知っておきたい統計学の基礎を学びましょう。
なお、それぞれの意味合いについては別項目で後述していくので、まずここでは原則として用語と計算方法だけを学び、リスクとリターンを学ぶ際の準備をしておきましょう。
【リスクとリターンを学ぶ上で必要な統計用語】
まず、リスクとリターンを学ぶ上で必要な統計用語とその概要を挙げてみます。
≪データが1種類の場合≫
まずはデータが1種類の場合です。
例えば入試の際の受験生の数学の得点を分析する場合などに使用します。
1.平均
平均は、誰もが知る統計の最も基礎的な概念です。
なお、ファイナンスでは「平均 = 期待収益率」となります。
平均(期待収益率) = データの値の総数÷データの個数
2.偏差
偏差とは、「平均からのばらつき」を意味します。
データの値から平均を引いたものです。
ファイナンス的には、このばらつきの大きさが「リスク」となっていきます。
偏差 = データの値−平均
3.分散
分散は、偏差を2乗してそれを加重平均したものです。
偏差はプラスとマイナスのばらつきがあるため、それをばらつきとして判断するには、2乗して記号の影響を排除しなければなりません。
この2乗したものが分散で、分散は必ずプラスの値となります。
そして偏差が大きければ必然的に分散も大きくなり、偏差が小さければ必然的に分散も小さくなります。
分散 = ((偏差)2の総和)の加重平均
4.標準偏差
標準偏差は分散の√(平方根)です。
分散は2乗しているので、それを√で戻したものが標準偏差です。
標準偏差 = √(分散)
標準偏差は分散を基準にしているので、結果的に標準偏差の値が「ばらつき =リスク」の大きさとなります。
≪データが2種類の場合≫
ここからは、データが2種類の場合です。
例えば入試の際の受験生の数学と理科の得点に関して、その因果関係を分析する場合などに使用します。
ここでは1種類目のデータをA、2種類目のデータをBと考えます。
5.共分散
分散が1つの統計に対して偏差を2乗したのに対し、共分散はAとBの2つの偏差を掛け合わせることで、偏差の積を計算したものです。
共分散 = Aの偏差×Bの偏差
共分散は分散とは異なり、別の数字を掛け合わせるので、記号はプラス、マイナスのどちらもあり得ます。
例えばAとBがともに平均以上の場合は偏差がプラス同士なので、共分散もプラスになります。
あるいはAとBがともに平均以下の場合も同様です。
そしてAとBのどちらかが平均以上で、どちらかが平均以下の場合は共分散はマイナスになります。
AとBの傾向が似ていればプラス、似ていなければマイナスということです。
6.相関
標準偏差が1つの統計に対する分散の√(平方根)だったのに対し、相関は共分散を「Aの標準偏差×Bの標準偏差」で割ることで、AとBの関係性を計算したものです。
相関には必ず分母のほうが大きくなるという特性があり、その値は必ず「−1」から「1」の間に収まります。
そして1に近ければ関係性は高い、0の場合は関係性がない、−1に近い場合は関係性が逆(反対)となります。
相関 = 共分散÷(Aの標準偏差×Bの標準偏差)
【統計の基礎的な計算】
では実際に計算してみましょう。
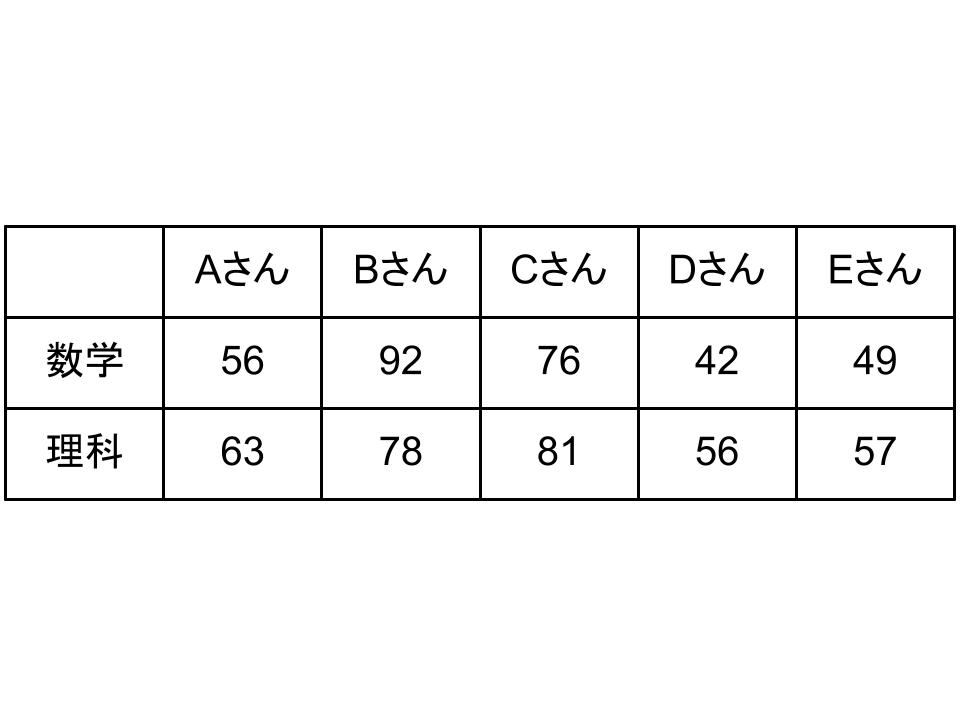
ここでは例として、入試を受けたA〜Eさんの数学と理科の結果について、それぞれの値を計算していくことにしましょう。
1.平均
ではまずは平均を出してみましょう。
≪数学≫
(56+92+76+42+49)÷5 = 63
≪理科≫
(63+78+81+56+57)÷5 = 67
数学は63点、理科は67点です。
2.偏差
次は偏差を見てみましょう。
偏差は「データの値−平均」です。
そして偏差はAさん〜Eさんのそれぞれのデータを個別に計算していきます。
まずは数学の偏差を出してみましょう。
≪数学≫
Aさん 56−63 = −7
Bさん 92−63 = 29
Cさん 76−63 = 13
Dさん 42−63 = −21
Eさん 49−63 = −14
プラスは平均以上、マイナスは平均以下です。
数学はBさんとCさんが平均以上でAさんとDさん、Eさんが平均以下となっています。
次は理科の偏差です。
≪理科≫
Aさん 63−66 = −3
Bさん 78−66 = 12
Cさん 81−66 = 15
Dさん 56−66 = −10
Eさん 57−66 = −9
理科についてもBさんとCさんが平均以上でAさんとDさん、Eさんが平均以下となっています。
ここまでで、ぱっと見ただけで数学と理科の点数には何らかの関係性があることが想像できます。
3.分散
次は分散です。
分散は偏差を2乗してそれを加重平均したものです。
よって偏差とは異なり、個別に計算されるのではなく、数学と理科でそれぞれ1つの値が計算されます。
まずは数学の分散です。
≪数学≫
最初に偏差を2乗してそれを加算したものを求めます。
(−7)2+292+132+(−21)2+(−14)2 = 49+841+169+441+196 = 1696
そして今回はこれをデータの個数で割ります。
分散 = 1696÷5 =339.2
次は理科の分散です。
理科は一気に求めてみましょう。
≪理科≫
分散 = ((−3)2+122+152+(−10)2+(−9)2)÷5 = (9+144+225+100+81)÷5 = 559÷5 =111.8
分散は「数学339.2>理科111.8」です。
4.標準偏差
つぎは標準偏差です。
標準偏差は分散の√です。
まずは数学の標準偏差です。
≪数学≫
標準偏差 = √339.2 ≒ 18.42
次は理科の標準偏差です。
≪理科≫
標準偏差 = √111.8 ≒ 10.57
ここまでで、「数学18.42>理科10.57」となっていることから、数学の点数のばらつきが理科よりも大きいことがわかりました。
ファイナンス的には、この値が大きいほうが「リスクが高い」ということになります。
5.共分散
次は共分散です。
ここからは2種類のデータを使用します。
ここではA〜Eさんそれぞれの数学と理科の2つの偏差を掛け合わせ、その加重平均を取ります。
実際に計算してみましょう。
Aさん (−7)×(−3) = 21
Bさん 29×12 = 348
Cさん 13×15 = 195
Dさん (−21)×(−10) = 210
Eさん (−14)×(−9) = 126
共分散 = (21+348+195+210+126)÷5 = 900÷5 =180
共分散はAからEさんのすべてがプラスとなり、180になりました。
共分散がすべてプラスということは、数学と理科の点数の関係性は高い可能性があるということです。
6.相関
最後に相関を計算してみましょう。
相関は、共分散を「数学の標準偏差×理科の標準偏差」で割ることで計算できます。
ここで、共分散は180、数学の標準偏差は18.42、理科の標準偏差は10.57です。
では実際に計算してみましょう。
相関 = 180÷(18.42×10.57) = 180÷194.6994 ≒ 0.925
相関は「0.925」です。
「1」に極めて近いため、数学と理科の点数の関係性は極めて高いことがわかりました。
【ファイナンスと統計】
ここまで、ファイナンスに必要な基本的な統計に関する用語とその計算方法を見てきました。
統計は主に投資におけるポートフォリオの決定やリターンの最大化を考える際には欠かせない考え方です。
そして今後のそれらの解説では、詳細な計算方法は省略されています。
よってまずはここで統計の用語や計算方法をしっかりとおさえ、そのうえでファイナンスの学習を進めていきましょう。
関連ページ
- 運転資金を即日調達する方法「ファクタリング」とは?【Q&A付き】
- 財務諸表とファイナンス その1
- 財務諸表とファイナンス その2
- 資金計画を考える
- ファンダメンタル価値理論と砂上の楼閣理論
- 資金調達方法(負債と自己資本) その1
- 資金調達方法(負債と自己資本) その2
- 資金調達方法(負債と自己資本) その3
- NPVによる投資評価 その1
- NPVによる投資評価 その2
- IR(インベスター・リレーションズ)とは
- IRR(Internal Rate of Return:内部収益率)
- リースファクター(年金現価係数) その1
- リースファクター(年金現価係数) その2
- 負債を活用した場合のNPV
- M&A(企業の合併・買収) その1
- M&A(企業の合併・買収) その2
- 企業経営とキャッシュフロー概念 その1
- 企業経営とキャッシュフロー概念 その2
- MVA(Market Value Added:市場付加価値)
- NPVの注意点
- 資本コスト算定の注意点
- NPVとAPVの関係
- NPV(Net Present Value:正味現在価値)
- CAPMの公式と解明 その1
- CAPMの公式と解明 その2
- 最適資本構成とMM理論 その1
- 最適資本構成とMM理論 その2
- オプションを理解する その1
- オプションを理解する その2
- 永続価値を理解する その1
- 永続価値を理解する その2
- PI(Profitability Index:収益性指標)
- ポートフォリオの拡張と最適ポートフォリオ
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その1
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その2
- プレミアムの算定(二項過程モデル、ヘッジレシオ、プット・コール・パリティ) その3
- 現在価値を理解する その1
- 現在価値を理解する その2
- 現在価値の計算
- 利益還元政策を理解する その1
- 利益還元政策を理解する その2
- 「格付け」を理解する
- リアルオプションを理解する
- リスクとリターン その1
- リスクとリターン その2
- リスクとリターン その3
- リスクを理解する その1
- リスクを理解する その2
- リスクとポートフォリオ その1
- リスクとポートフォリオ その2
- 証券化とは
- ファイナンスのための統計学基礎
- 経営戦略とファイナンス その1
- 経営戦略とファイナンス その2
- 埋没コストと機会費用
- 株価の理論値を理解する その1
- 株価の理論値を理解する その2
- バリュエーションを理解する
- 資本コスト(WACC)を理解する その1
- 資本コスト(WACC)を理解する その2
- ブラック-ショールズの公式
- 回収期間(Payback)法と会計上の収益率 その1
- 回収期間(Payback)法と会計上の収益率 その2
- 株主に報いるには
- ファイナンスとは
- 「儲け」とは
- APV(Adjusted Present Value:調整現在価値)
- β(ベータ)を理解する
- CAPM(Capital Asset Pricing Model)とは
- キャッシュフローを理解する その1
- キャッシュフローを理解する その2
- キャッシュフローを理解する その3
- 連結決算が企業価値に与える影響
- コーポレートガバナンス(企業統治)を理解する その1
- コーポレートガバナンス(企業統治)を理解する その2
- 企業価値を理解する
- 負債コストとオプションの関係
- 経営の多角化が企業価値に与える影響
- 効率的市場仮説とランダムウォーク
- EVA(Economic Value Added:経済的付加価値)
- 財務レバレッジとβ(ベータ) その1
- 財務レバレッジとβ(ベータ) その2
- 財務レバレッジとβ(ベータ) その3
- 財務政策を理解する
