交互進行ゲーム(逐次手番ゲーム)とゲームの木
「囚人のジレンマ」では2人の囚人は互いにどんな選択をするのかがわからない状況に置かれていました。これは「男女の争い」や「チキンゲーム」「居酒屋ゲーム」でも同様です。これらのゲームを「同時進行ゲーム」と言います。
対して「交互進行ゲーム」とはあるプレイヤーが戦略を選んだ後に、別のプレイヤーが戦略を選ぶというもの。ここには同時進行ゲームにはない、「時間の経過」という概念が生まれます。
交互進行ゲームは「逐次手番ゲーム」とも言います。それでは具体例を見てみましょう。
例題1
ある商店街に唯一残るケーキショップXは、その一帯のケーキ需要を独占していました。しかしある時、低価格で有名な隣町のケーキショップYが商店街に出店するかを検討している、という情報が流れてきます。
Xが取り得る戦略は「高級路線に切り替える」か「低価格路線を打ち出す」かの2つだとしましょう。
Yが商店街に出店しない場合にはXが商店街のケーキ需要を独占し続け、Yが出店しXが「高級路線に切り替える」を選んだ場合には利益を半分ずつに分け合い、Xが「低価格路線を打ち出す」を選ぶと、互いに消耗しあって損失を出すと仮定します。
解説
この意思決定の構造を図示したものが下図です。
1.jpg)
このような図を「ゲームの木」と呼びます。このゲームにおいてXの選択肢は「高級路線に切り替える」か「低価格路線を打ち出す」かの2つだけではありません。
相手の出方を見た後に戦略を選べるため、「Yが参入すれば高級路線に切り替える」「Yが参入すれば低価格路線を打ち出す」「Yが参入しなければ高級路線に切り替える」「Yが参入しなければ低価格路線を打ち出す」という4つの選択肢があります。
このように、将来自分が戦略を選ぶ時点において、自分が持っている情報に基づいた行動を、実際には起こらない場合も含めて全て列挙する「条件付き行動計画」が、交互進行ゲームの戦略の特徴です。
例題2
PとQがカードゲームをしています。それぞれ白と黒のカードを持っており、まずPが白か黒のカードを選び、それを見た上でQがカードを選びます。
Pが白を選び、Qが白を選ぶとPには10ポイント加算されますが、Qにはポイントが加算されません。対してQが黒を選べばPとQに1ポイントずつ加算されます。
Pが黒を選び、Qが白を選べばPは0ポイント、Qは3ポイント、Qも黒を選べばPは4ポイント、Qは2ポイント加算されます。この状況での意思決定はどのようになるでしょうか。
解説
下図がこのケースの意思決定の構造を図示したゲームの木です。Qは相手の出方を見た上で自分の戦略が選べるので、このゲームは交互進行ゲームと言えます。
2.jpg)
QからすればPが白を出した場合には黒を出すでしょうし、Pが黒を出せば白を出すでしょう。それが最も得をする戦略だからです。ではこのときPは始めにどちらの戦略を選べば、より多くのポイントが得られるでしょうか。
答えは白です。黒を選べばQは自分が最大になるように白を選ぶでしょう。その時Pのポイントは0です。これを防ぐには白を選ぶしかありません。白を選べば最低でも1ポイントは手に入れられるからです。
このように交互進行ゲームでは自分の戦略ごとの相手の出方を予測して、自分の戦略を決定することもできます。
ゲームの木とは
ゲームの木とは「交互進行ゲーム」において非常に重要なツールです。同時進行ゲームでは利得表を用いて意思決定をしたりゲームの構造を把握したりしましたが、交互進行ゲームではこのゲームの木を用います。
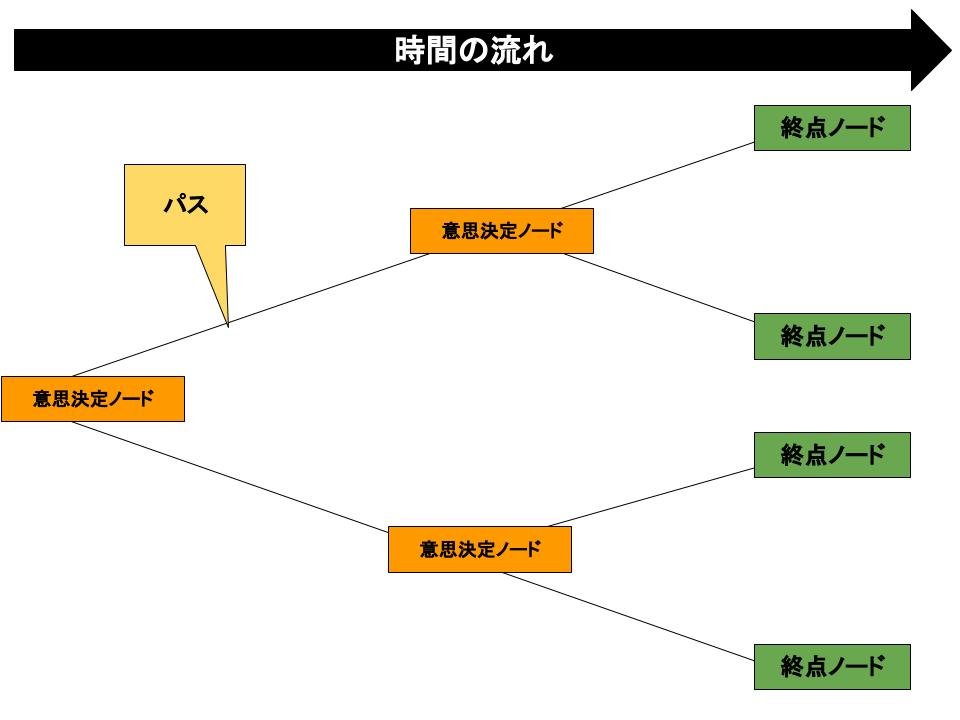
ゲームのスタート地点は図の左端の部分。右に移動するにつれて時間が経過していき、各分岐点には意思決定を行うプレイヤーの名前が書かれています。
この分岐点を「意思決定ノード」と呼び、意思決定ノードから伸びる枝を「パス」と呼びます。ゲームの木の1番右端の部分を「終点ノード」といい、ここにそれぞれの利得が書かれます。
ゲームの木の具体例
図1は「交互進行ゲーム(逐次手番ゲーム)」で例に挙げた2店のケーキショップの意思決定を示したゲームの木です。XとYがそれぞれ選択を行っている場所が意思決定ノードで、「出店する」「出店しない」「高価格路線」「低価格路線」がそれぞれパスです。
終点ノードにはそれぞれの利得が書かれており、どの選択肢を選べばそれぞれのケーキショップがどのような利得が得られるかが一目で理解できます。
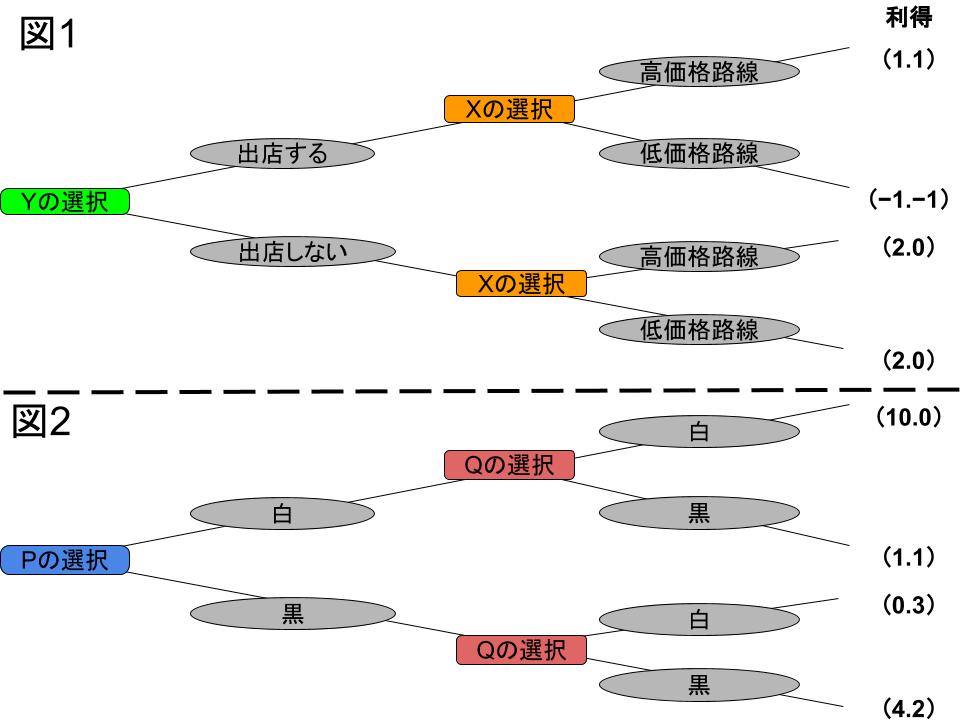
これは白と黒のカードをめぐるPとQの意思決定でも同じことが言えます(図2)。「Pの選択」「Qの選択」と書いてあるところが意思決定ノード、「白」「黒」と書かれているのがパスです。
どちらの例でも後に戦略を選ぶプレイヤーの方がゲームの鍵を握っているように見えます。しかしゲームの木を書いてゲームを俯瞰すると、始めに戦略を選ぶプレイヤーは、後に戦略を選ぶプレイヤーの意思決定を見越して意思決定できることがわかるはずです。
では以下の例に従って、実際にゲームの木を自分で書いてみましょう。
例題1
L市は「たこ焼きの聖地」と呼ばれています。同地ではK店というたこ焼き屋が圧倒的なシェアを誇り、L市でたこ焼きといえばK店を指すほどでした。K店もL市で創業したので、本社を同地に置き、地域との絆を大切にしています。
しかしある時T店という大手全国チェーンがL市に出店してきました。K店の圧倒的優位はわかりきっていましたが、T店としても「たこ焼きの聖地」に出店してブランドイメージをより強化したいと考えての決断でした。
ところが出店から6ヶ月後、T店の経営は軌道に乗らず、撤退か残留かの選択をせまられる状況になってしまいます。
それを横目で見ていたK店の社長は「T店は確かに実力のある店舗だ。彼らと協調路線をとればK店のメリットになるかもしれない。しかしK店のブランドイメージもある。協調路線をとるよりも、むしろ潰しにかかる方がいいのかもしれない。どうしたものだろうか」と悩みます。
対して撤退か残留かを悩むT店の社長は残留する場合はK店との協調路線をとりたいと考えていますが、仮に交渉が決裂し、K店がこちらを潰しにきた場合、どのように対応するのかについても考えていました。
「その時点で撤退すれば最小限の損失で止められる。もし応戦すればこちらも大きな損失を被るが、K店にも少なくない損失を与えられるだろう。どうしたものだろうか」
もしT店が始めの段階で撤退していればT店にはなんとか1億円の利益が残り、K店には9億円の利益が入ります。
T店が残留し、かつK店が協調路線をとった場合にはT店には3億円の利益、K店には7億円の利益が入ります。
もしK店がT店を潰しにかかり、それにT店が恐れをなして撤退した場合、T店は1億円の損失を被るのに対し、K店が得る利益は8億円です。
T店が心中覚悟で応戦すれば双方5億円の損失を被ります。
さてこの場合のゲームの木はどのようになるでしょうか。
解説
答えは下図の通りです。複雑な文章でも「意思決定ノード」と「パス」、「終点ノード」における利得関係を把握していれば、ゲームの木にすることは可能だということを覚えておきましょう。
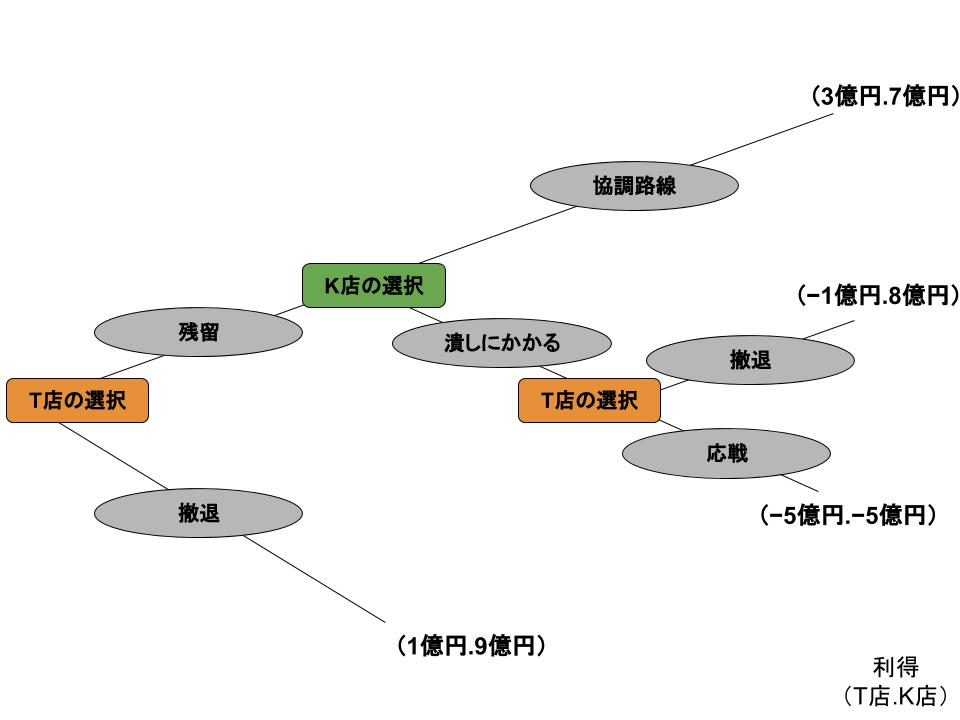
ちなみに、この場合K店が8億円の利得を得ようとして潰しにかかってくる可能性があるので、T店ははじめから撤退するのが賢い選択のように思われます。
まとめ
・交互進行ゲームは「あるプレイヤーが戦略を選んだ後に、別のプレイヤーが戦略を選ぶ」ゲーム
・交互進行ゲームには「時間の経過」という概念がある
・交互進行ゲーム=逐次手番ゲーム
・交互進行ゲームの戦略は「条件付き行動計画」
・交互進行ゲームでは相手の出方を見てから判断できるとともに(例題1)、自分の戦略ごとの相手の出方を予測して、自分の戦略を決定することもできる(例題2)
・ゲームの木の構成要素は「意思決定ノード」「パス」「終点ノード」
・複雑なゲームでも、ゲームの木を書けばプレイヤーがどのような選択をすればゲームがどのように進行するのかが一目でわかる
関連ページ
- ゲーム理論とは…意味を理解してビジネスの駆け引きの現場で活かす
- 交互進行ゲーム(逐次手番ゲーム)とゲームの木
- ゲーム理論の視点からオークションの仕組みを理解する
- ベイズ均衡(ベイジアンナッシュ均衡)
- 男女の争いとチキンゲーム
- コーディネーションゲーム(失敗と解決法)
- クールノー競争とベルトラン競争
- ゲーム理論の基本を理解する(囚人のジレンマ)
- ホテリングの立地ゲーム
- 情報非対称ゲーム(不完備情報のゲーム)
- ミニマックス定理
- 混合戦略と純粋戦略
- ナッシュ均衡を理解する
- 部分ゲーム完全均衡と後ろ向き帰納法
- 囚人のジレンマの解決法
- 戦略形ゲームのモデルを理解する
- 脅しのゲームと信頼のゲーム
- 交互進行ゲームにおける戦略と信頼性のない脅し
