ミニマックス定理

トップページ＞ゲーム理論＞ミニマックス定理

ミニマックス戦略とはゲーム的状況において、「自分の損失を最小限にとどめるための戦略」を言います。

私たちは日々多くのゲーム的状況に直面しますが、その全てにおいて自分にとって最大の利得が得られる戦略を選べるわけではありません。

しかしそうなった場合に一番損失の少ない選択肢を選ぶことができれば、最悪の事態を回避することはできます。したがってミニマックス戦略は「次善策（セカンドベスト）」として、ゲーム的状況において重要な役割を果たすのです。

ミニマックス定理とゼロサムゲーム

ミニマックス戦略が有効になるのはとるかとられるかの「ゼロサムゲーム」においてです。

ゼロサムゲームにおいては一方に10の利得があるとき、もう一方には10の損失があります。つまりプレイヤーの得点（＋10）と失点（−10）の総和（サム）が0になるゲームです。

このような性質上、ゼロサムゲームで自分がミニマックス戦略を選択した場合、相手の利得は最小限になります。このような「相手の利得を最小限にとどめるための戦略」がマックスミニ戦略です。

つまりプレイヤーは「自分の損失を最小限にとどめるための戦略」であるミニマックス戦略を選ぶとき、同時にマックスミニ戦略を選んでいるのです。

ミニマックス戦略とマックスミニ戦略が表裏一体であることを「ミニマックス定理」と呼びます。

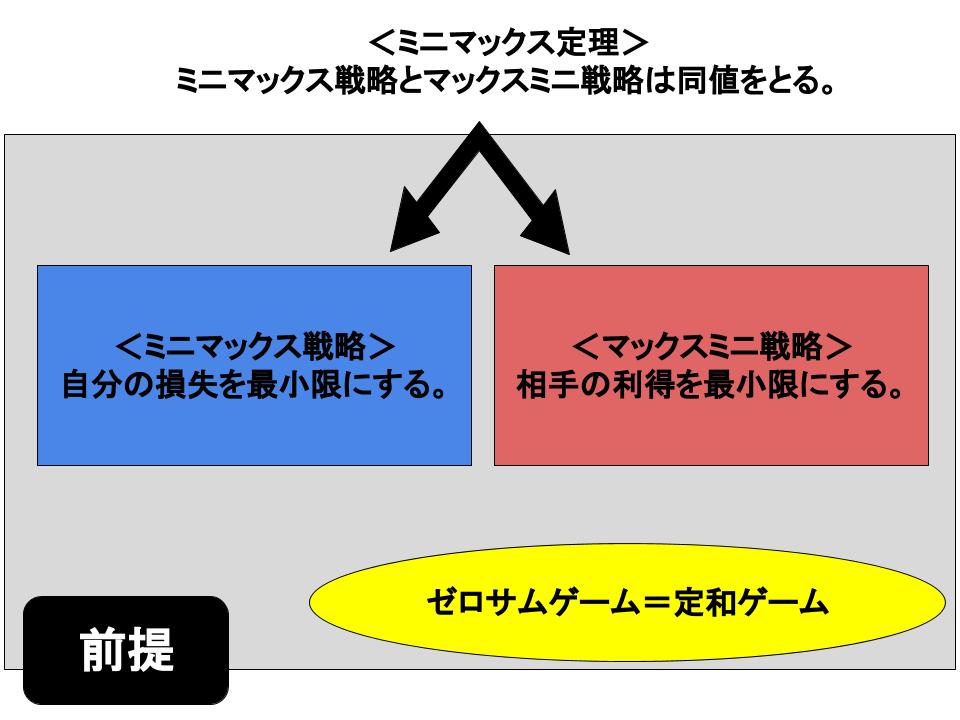
ミニマックス定理

ここまでの内容をまとめた概念図が上図。具体的に理解するために、以下で例をあげて見てみましょう。

例題1

ある村の村長選挙でXとYが立候補者として名乗りをあげました。Xは最近この村に移住してきた人物ですが、以前は大手広告代理店で手腕を振るっていたという経歴から、村に新しい風を吹かせたいという村民から期待を寄せられています。

対してYは昔からこの村で暮らしている豪農で、農業従事者からの厚い信頼を勝ち取っている人物です。今のところ2人の支持率は50％ずつ。どのような政策を打ち出すかで勝負が決まる状況です。

現在の村は2つの大きな問題を抱えています。1つはかつて村の主要産業であった農業の衰退。荒れた田畑が増えたせいで収穫高が減少しているのです。しかし農業で生計を立てる村民も多く、打開策が求められています。

2つ目の問題は人口減少です。10年ほど前から人口減少が進み、このままでは遅かれ早かれ村自体がなくなってしまいます。本来であれば両方の問題を解決するべきですが、村の予算の関係上、候補者はどちらかの政策を選ばなくてはいけません。

XとYがともに「農業政策」を打ち出した場合、Xの支持率はマイナス15％、Yの支持率はプラス15％となります。Xが「農業政策」を、Yが「人口政策」を打ち出した場合の支持率はXがプラス20％、Yがマイナス20％です。

Xが「人口政策」を、Yが「農業政策」を打ち出すとXの支持率がプラス5％、Yの支持率がマイナス5％となり、両方が「人口政策」を打ち出すと支持率は変化しません。

解説

ミニマックス戦略は次の手順で導きます。

1. ミニマックス戦略を導きたいプレイヤーを決める。

2. 相手プレイヤーの各戦略における、1のプレイヤーの利得が最小になる戦略を見つける。

3. 2で見つけた「利得が最小になる戦略」のうち、より利得が大きい方がミニマックス戦略となる。

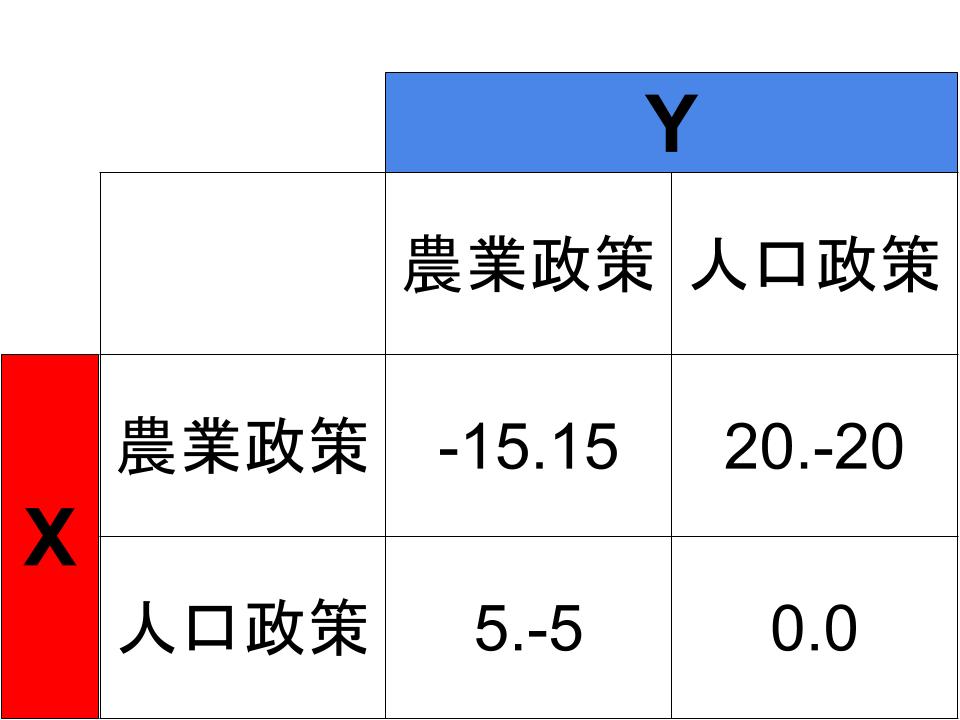
ミニマックス定理2

このゲーム的状況を利得表にしたのが上図です。一方が獲得した支持率の分だけ、一方の支持率が低下しています。つまりこのゲームは「ゼロサムゲーム」です。

それでは上述の手順に従って、Xのミニマックス戦略を考えてみましょう。Yが「農業政策」を打ち出した場合のXの「利得が最小になる戦略」は支持率がマイナス15％になる「農業政策」です。

対してYが「人口政策」を打ち出した場合、Xの「利得が最小になる戦略」は支持率の増減がない（0％）の「人口政策」となります。したがってXのミニマックス戦略は「人口政策」です。

この時の「0％」を「Xのミニマックス値」と言います。Xがミニマックス戦略を選択した場合、Yはより利得の多い「人口政策」を選ぶはずです。

するとYの利得は、Yが元々得ることができた利得（プラス15％か0％）のうち、最小の「0％」となります。これはXがミニマックス戦略（人口政策）を選択したことにより、Yはマックスミニ戦略（人口政策）を選択せざるをえなくなってしまったのです。

このようにミニマックス戦略とマックスミニ戦略は同じ戦略を意味するのです。

ゼロサムゲームと定和ゲーム

プレイヤーの利得の和が一定の数値を示すゲームを「定和ゲーム」と言います。ゼロサムゲームはプレイヤーの利得を足すと常に0になるため、定和ゲームです。

対してプレイヤーの利得を足しても数値が一定にならないゲームを「非定和ゲーム」と呼びます（非定和ゲームは同時に「非ゼロサムゲーム」でもあります）。

ミニマックス戦略とナッシュ均衡

ミニマックス戦略が有効になるのはゼロサムゲームにおいてです。先ほどの村長選挙で見たように、ゼロサムゲームでミニマックス戦略を選択すると「プレイヤー全員が相手の戦略に対する最適反応を選んでいる状態」、すなわちナッシュ均衡になります。

しかし、これが非ゼロサムゲームだった場合には、ミニマックス戦略ではナッシュ均衡は導き出せません。次の例題で、これがどういうことなのかを具体的に見ておきましょう。

例題2

営業マンのPは取引先のZ社に対して、自社製品を売り込みに行くべきか、行かざるべきかで迷っています。Z社の担当者は非常に製品を見る目が厳しく、なかなか買ってくれないことで有名です。

対してPは自分の営業力に自信がなく、とてもZ社の担当者に首を縦に振ってもらえるとは思えませんでした。とは言っても売り込みに行かなければ決して製品は売れません。

しかしZ社の担当者は「本当に価値のある製品は積極的に採用したい」と考えており、できるだけ多くの営業マンの話を聞きたいと思っています。

解説

この状況を利得表にすると、下図のようになります。PがZ社に営業をかけ、Z社の担当者が製品に魅力を感じて採用すれば、両者にとってはプラスが生まれます。

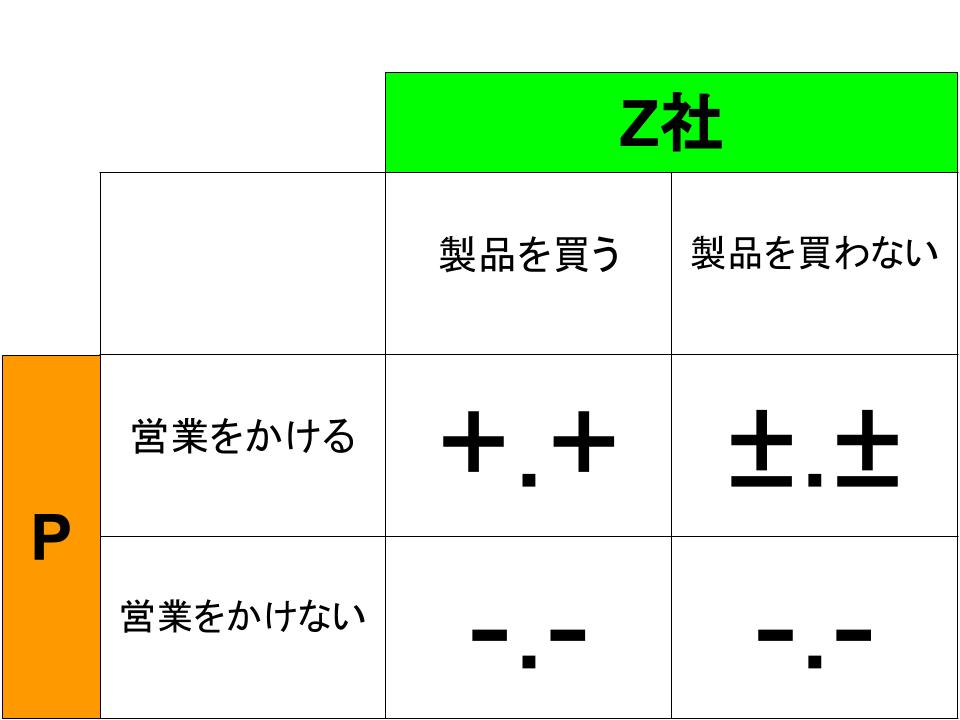
ミニマックス定理3

確かにPが思い切って営業をかけたにもかかわらず、Z社の担当者が納得しなければ製品は売れませんが、Pにとって何か損失が起きるわけでもなく、またZ社にとっても損失はありません。

しかし、もしPが「営業をかけない」という判断をしてしまえばPとZ社、両方にとって「機会損失」が生まれます。つまりPにとってはZ社の担当者が製品を買おうが買うまいが、営業をかけるのが最善の戦略なのです（「支配戦略」）。

ではこのゲーム的状況において、ミニマックス戦略を考えるとどのような結果になるでしょうか。

Z社が取引をすると決めている場合、Pに最大損失をもたらすのは「営業をかけない」という戦略です。またZ社が取引をしないと決めている場合のPに最大損失をもたらすのも「営業をかけない」という戦略です。

よってPのミニマックス戦略は「営業をかけない」になってしまいます。しかし先ほども見たようにPの最善の選択肢は「営業をかける」。ミニマックス戦略とは一致しません。このように、非ゼロサムゲームではミニマックス戦略はナッシュ均衡を導き出せないのです。

まとめ

・ミニマックス戦略とは「自分の損失を最小限にとどめるための戦略」である

・マックスミニ戦略とは「相手の利得を最小限にとどめるための戦略」である

・ミニマックス戦略とマックスミニ戦略が一致することを「ミニマックス定理」と言う

・ミニマックス戦略はゼロサムゲームのみに有効で、非ゼロサムゲームでは使えない

・プレイヤーの利得の和が一定値になるゲームを定和ゲームと言い、一定にならないゲームを非定和ゲームと呼ぶ

・ミニマックス戦略に対応する損失（利得）をミニマックス値と呼ぶ

・ミニマックス戦略の導き方
1. ミニマックス戦略を導きたいプレイヤーを決める
2. 相手プレイヤーの各戦略における、1のプレイヤーの利得が最小になる戦略を見つける
3. 2で見つけた「利得が最小になる戦略」のうち、より利得が大きい方がミニマックス戦略となる

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど