統計学の基本的な考え方…確率分布・標本抽出
統計とはなんでしょうか。それは、大量のデータの中に、ある法則性を見つけ出す分析手法です。自然科学や社会科学、人文科学などの研究をするときに用いられており、統計学という学問体系が整理されています。
学問だと言われ、慣れない専門用語に数式が必要な分析手法だときけば、難しそうだと考えてしまいます。しかし、基礎からしっかり学んでいけば何も怖くありません。
まずは、おおまかな概念を理解するようにしましょう。基本的な考え方は、次の2つです。
1. すべての統計的現象は、確率分布をする。
2. すべての統計的現象は、母集団を観察する代わりに標本を観察して、それをもとに母集団の特性を推測して分析する。
(出典:「はじめての統計学(日本経済新聞出版社)」著:鳥居泰彦)
すべての統計的現象は、確率分布をする
言葉の定義について、話をすすめます。「分布」と「確率」です。最初に、分布とは、ある現象がさまざまな大きさで存在することを指します。
同一年齢の小学生のクラスを背の順に並べる様子を想像してみましょう。「学年は一律ですが、身長は分布する」という表現を使います。同様に考えれば、「人の寿命は分布する」「同一年齢の給与水準の分布は…」といった使い方ができます。
次に、確率とは、ある現象がおこる確からしさを割合で示したものです。「明日の降水確率は80%です」や「野球選手の打率は2割5分です」といった使い方をします。
ここで、「分布」と「確率」を組み合わせて考えてみましょう。例として、小学4年生を100人集めた場合、そのうち35人の身長が130〜140?にあるという架空の状況について言い換えてみます。
身長は分布するものであり、一定の範囲に入る人数は割合によって表現できるものです。このとき、「小学4年生の身長が130〜140?である確率分布は35%です」という表現をします。
この確率分布を、グラフで表現してみましょう。身長を一定の間隔で区切り、対象人数と割合を一覧表にして、度数分布表にしてみます。
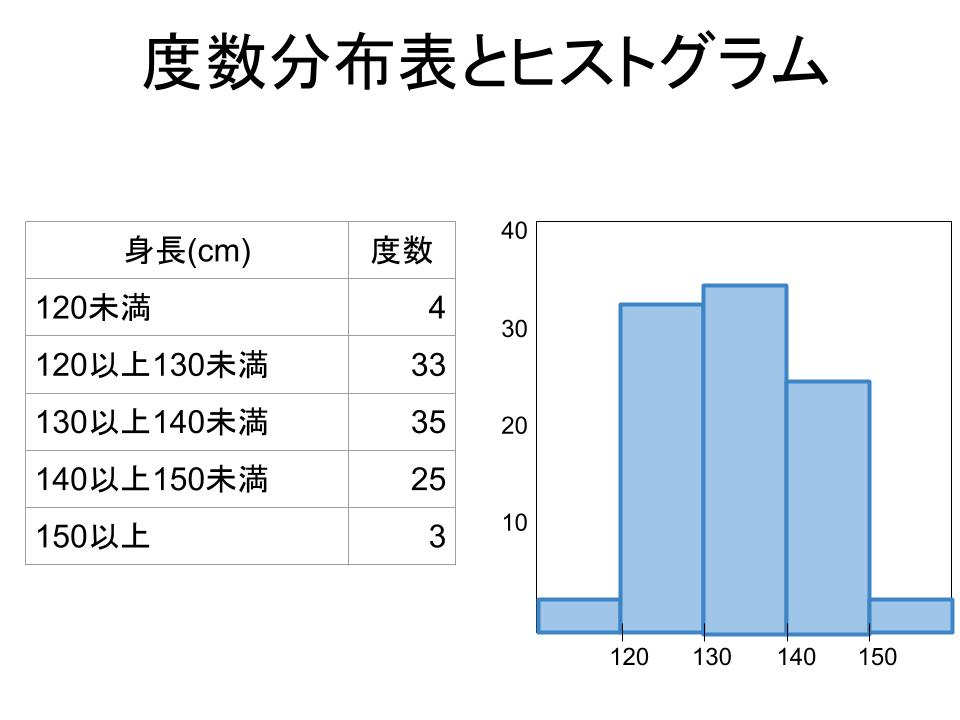
グラフの横軸は、身長の区分です。統計用語では、変数値と呼ばれます。縦軸は、度数と呼ばれます。度数は、人数であれば絶対度数と呼ばれ、割合であれば相対度数と呼ばれます。
統計の分野では、確率はPとあらわされます。ヒストグラムの例でいえば、身長Xが130cm以上140cm未満である確率Pは0.35である、と表現します。
標本観察をもとに母集団の特性を推測して分析する
言葉の定義について、話をすすめます。「母集団」とは、観察したい対象のすべてを指します。「標本」とは、観察したい対象の一部を指します。母集団をすべて観測したいと考えてもコストや手間がかかり、現実的には難しいものです。そこで、母集団から標本を抽出することで、全体を推計できるようにしたのが統計学の基本的な考え方の2つ目です。
標本として抽出するときには、一般的には乱数表を用います。ここで注意しなければならないのが、一部抽出した標本調査が必ずしも母集団全体をあらわすわけではないということです。
調査結果が誤差を含むということを考慮したうえでその確率を示し、予測を行います。全体を調査していないのに、一部の調査だけで結論を見出すのは飛躍しすぎではないか、と感じられるかもしれません。
しかし日常生活のなかでも、調理の味見をするときや、無料お試し期間で機能制限された中でサービスを活用するときなど、一部のお試し行動であっても全体を考慮して可か不可の意思決定を行っていることはよくあるのです。
母集団に対してどの程度の標本数が必要かについては、求める精度に応じて計算によって導き出すことができます。これが70%の確率であるならば、施策を意思決定することは難しいかもしれません。
しかし「標本誤差」では、「95%の確率で〇〇である」といった結論を導くことができます。ビジネスの意思決定の場において、全量調査ができなくても一部の分析で母集団を推測できることは、とてもメリットがあります。
サンプルの選び方:標本抽出(有意抽出と無作為抽出)
サンプルの選び方にはいくつか方法がありますが、統計学では標本抽出と呼びます。ここでは、標本抽出について考えてみます。
母集団には2種類ある(有限母集団と無限母集団)
観察したい対象を母集団と呼びます。時間とコストをかけても全数調査できるようなデータ集団のことを「有限母集団」と呼びます。ある日時における日本の人口を調査対象とすることは有限母集団です。
一方、実験室で繰り返されるようなことや、サイコロを振り続けるように制限なく繰り返すことが可能な調査対象を、「無限母集団」と呼びます。
標本の抽出方法は2種類(有意抽出と無作為抽出)
観察したい対象を母集団と呼びますが、全体調査ができないことがあります。このとき一部を抜粋して標本とし、母集団の特徴を推察する方法を推測統計学と呼びます。母集団とのずれが小さく意味のある推測をするためには、どのように標本を選ぶかが重要です。
このときデータの抽出方法には2種類あり、「有意抽出」と「無作為抽出」があります。
1.jpg)
有意抽出とは、知見者の判断で母集団の代表だと思えるサンプルを主観的に選ぶ方法です。誤差が大きくなることがあるので、あまり用いられることはありません。
一方の無作為抽出は、ランダムに標本を選ぶ方法です。一般的に、標本といえば無作為抽出する方法がとられます。この無作為抽出には、2通りあります。一度に標本全部を抽出する「非復元抽出」と、抽出しては母集団に戻す「復元抽出」です。
当たりくじを例にすれば、くじを引くたびに元に戻す復元抽出では、当選確率は常に一定です。戻さない非復元抽出では、毎回確率は変わります。
では、日本人の月間所得を調べるために1,000世帯を抽出したい場合にはどうしたらよいでしょうか。一つの母集団に対して標本抽出を行うことを「単純抽出法」と呼びます。
しかし、世帯が各地に散らばってしまうと、調査に時間と手間がかかります。まず、都道府県の選択をして(20県)その都道府県のなかから(50世帯)を抽出します。このように、階層を持たせた場合には「層化抽出法」と呼ばれます。
無作為抽出する方法としては、母集団の要素に番号をつけ、乱数表によりランダムに標本選出する方法がとられます。現在はコンピューターで乱数表を容易につかえるため、扱う数量が多くても簡易に行うことができます。
非標本誤差|調査プロセスで発生する誤差
一部のサンプルから全体を推計する推測統計学では、一定の誤差が発生します。ただし、母集団とあまり変わらない範囲を数学的な思考で指定することができるので、その誤差が許容範囲であるかどうかを判断してから分析を進めることができます。
しかし、実際の調査の過程では、単純ミスやサンプルの偏り、設問や回答の偏りなどが発生することがあります。これは統計学とは関係ない事象なので計算上は考慮されないのですが、注意が必要です。
気が付かないことが重大な誤差につながることもあるのです。いくつか、気を付ける点をあげます。
非標本誤差の種類|単純ミスを防ぐ
記録間違いやデータ入力ミスを防ぐために、ダブルチェックを行うなどの方法でカバーします。
非標本誤差の種類|低い回収率はサンプルの偏りに注意する
アンケートの回収率が低い場合、母集団に近しい集計にならない場合があります。例えば商品の使用感についてのアンケートでは、良い印象を持っていると回答が集まり、使いにくい印象をもっていると回答しづらく調査協力に否定的になりがちです。
そのため、本来の結果と異なる逆転現象が起こりやすいのです。なるべく多くの回答を得られるようにしましょう。
非標本誤差の種類|回答の偏りはないか
対面調査で成績を問う時、実際よりすこし良い評価を答えてしまうことなどが考えられます。また、設問に対して回答項目に過不足があるときちんと答えることができなくなります。
