ビジネス統計学とは…なぜ今、統計学を学ぶ必要があるのか
ビッグデータ時代といわれる現代のビジネス環境では、データ分析の能力がさまざまな場面で求められます。そこでこの記事では、ビジネスの現場で役立つデータ分析の基礎である、ビジネス統計学について解説していきます。
統計学の歴史
統計学とはどのような学問なのでしょうか。現代にいたる統計学の歴史には3つの源流があります。その目的とは、「国の実態をとらえること」「大量の事象をとらえること」「確率的事象をとらえること」でした。

紀元前の古代エジプト王朝では、人口調査や食料配分、氾濫するナイル川流域の土地区画再整備の測量ために統計的な手法が用いられてきました。人類の文明の歴史とともに、統計学は生まれてきたのです。
また、古代ローマにおいて人口や所得の調査、財産の評価などを担当する職員をCencorと呼んでいました。センサスとは調査という意味ですが、この語が語源になっています。18世紀から19世紀(デンマーク1769年、アメリカ1790年、オランダ1795年、イギリス1801年)にかけて、各国で現代的な調査が行われるようになってきました。
日本での政府統計は、現在総務省が取り扱っています。国勢調査は日本に住む人の調査を行い、経済センサスは事業所・企業の情報をとりまとめるために実施されています。
イギリスのジョン・グラントは、ペストの度重なる流行があったロンドンで死亡統計表を分析しました。その結果、当時200万人と予測されたロンドンの人口について、約34万人であると推計をしました。
また、ハレー彗星で有名なエドモンド・ハレーは、偶然によると考えられていた人類の死亡について、一定の規則性があることを示しました。これにより、合理的な計算をもとにした生命保険ビジネスの発展につながったのです。
前述の国勢調査は、全数調査で国の実態をありのまま明らかにすることに主眼を置いたものですが、こうした物事の状況を把握するにとどまらず、複雑で大量な物事の背景にある規則性を指摘することは大きな違いです。
サイコロやトランプゲームによる賭博の研究に、16世紀ごろから数学的な要素を用いるようになりました。地動説を唱えたガリレオも「サイコロゲームについての考察」という論文を発表しています。ここから確率論の基礎がうまれ、期待値、推定、検定、標本理論といった手法に発展しました。
18世紀になると、条件付き確率を導いたベイズ理論が生まれます。これは、事柄Aがおきたことを前提に事柄Bがおこる確率をもとめるもので、人間の勘や経験を確率に埋め込むことができます。トランプでスペードが出たときに絵札である確率は、「3 ÷ 13」であるというものです。
19世紀になると、これらの手法がまとめられるようになり、統計学は社会現象・自然現象に共通して用いられるようになりました。20世紀になるとテクノロジーが進化し、複雑で時間を要する計算をコンピューターが代替してくれるようになります。ITにより情報処理のスピードが格段に速くなったのです。
ビジネス領域の中ではマーケティングの現場で、統計学の中でも新しいデータマイニングの技術が発展してきます。そこで求められる事例は、例えば「蓄積された消費者の購買データ群の中から、まだ知られていないが、売上向上に有益な商品の組み合わせを見つけ出すこと」です。
これをバスケット分析と呼びます。また、営業報告からテキストマイニングをし、失敗事例につながる要注意の単語をピックアップし、成功に導くような事例もあります。このように21世紀の現在には、身の回りの様々な事象から最適解を予測しビジネスの発展につなげる目的で、統計学の知識が応用されるようになってきました。
統計学の種類|記述統計とは
ある時代や地域のデータの集まりに対して、何かしらの端的な特徴を調べる方法を記述統計学と呼びます。例をあげれば、人口調査や土地調査は古くから行われており、17世紀ごろには出生率や死亡率といったデータを研究する書物が発表されていました。
また、現代におけるGDPや大学の偏差値も記述統計学であり、私たちがよく利用する「平均値」や「標準偏差」、ヒストグラムから導かれる「最頻値」といった単語には、なじみがあるでしょう。
統計学の種類|推測統計とは
一方、統計学と確率理論を組み合わせて、一部のデータから全体を推測する手法を推測統計と呼びます。これは、20世紀以降に開発された方法で、現代では選挙速報や保険商品などに用いられています。
統計は過去に観測されたデータの集まりを取り扱いますが、確率は未来におきることを推測したものです。選挙速報で開票が始まってすぐに当確が発表されるのは、95%の割合で未来をほぼ予測できる推測統計を用いているからなのです。
「多変量解析」は、推理統計学の一分野で、変量が多くある場合に用いられる手法です。ビジネスにおいては、商品や宣伝手法などさまざまな要素が売上につながります。
ビッグデータの解析などでは、行列やベクトル・微積などの数学的な手法を用いて要素の関係性を調べ、有益な情報を統計学的に導き出そうとするときに活用されます。
ビジネス統計学が生み出すチャンス
意思決定しなければならない場面において、私事であれば勘や経験で決めてしまってもよいでしょう。しかし、ビジネスの現場において、株主や顧客などステークホルダーとの関係性により、合理的な判断が求められることがあります。
このようなときに、勘や経験で物事を進めようとしても相手を説得することは難しいでしょう。意思決定の根拠として、数値データに基づく論理が求められているのです。
ビジネスロジックやフレームワークを用いて分析するほか、データ分析によって意思決定の判断材料にするのにさまざまな方法があります。固定費と変動費に分けて収益構造を比較したり、シェアや売上・収益構造の差分分析を行ったりします。
また、ある項目値を時系列の折れ線グラフで表現して、大きな流れを見つけ出す分析など、利用シーンは多く浮かびます。
ここで、営業所や営業担当別に同一商品の販売価格を比較すると、標準価格に近い値段を維持できている場合や、値引き対応により値崩れがおきている場合などがみられます。
度数分布表をもちいて最頻値を見つけ出す売価分布のヒストグラムを作成すれば、視覚的にわかります。このように、バラつきがみられるデータ分析や、未来の予測を確率論で語りたいときなどにビジネス統計学が利用できます。
ビジネスデータを統計分析すれば、過去に起こったことから規則性を見出し、未来の予測を一定の誤差の範囲で推定することができます。
プロスポーツの分野では、選手の動きをセンサーで感知して勝利に導く戦術により、ゲーム観戦する観客はより面白みを感じられるようになり、ファンを増やすことも可能でしょう。
店舗を構える小売業では、顧客の会員カード情報とPOSデータから、またユーザーの居住エリアやリピートする商品から、特別セールのDMを効率的に配信することができます。さらにWEBサービスの分野では、検索エンジンやログデータからリアルタイムに追跡広告を表示させることも可能です。
物流ではRFIDタグを活用した非接触でのデータ読み書きにより、効率的に倉庫スペースを活用し、農業においても環境データの蓄積から、生育にあわせた最適な対処をすることができるようになってきています。
IT技術の進歩がよりビジネス面でも注目されるに従い、データサイエンティストの不足が懸念されるようになってきました。
データサイエンティストに求められるのは、ビジネスの背景を十分に理解したうえで必要なデータを整え、統計学や情報処理の能力を駆使して運用し続けていくことです。使用する分析ツールは素人でも扱えるソフトウェアもありますが、多少のプログラミングの知識は必要です。
このほか、企業に蓄積された情報はデータベースに格納され、統合ツールとして大規模化している傾向にあります。このような環境で求められるデータサイエンティストになるには、情報工学や計量経済学、金融工学などの専攻者が有利です。
しかし、データサイエンティストでなくても、ビジネス統計学を学んぶことはとても重要です。21世紀のビジネスシーンで生き残っていくには、ビッグデータをどう活用していくかという問題と向き合わなくてはなりません。
統計学はどのように社会の役に立ってきたのか
それでは、実際に統計学はビジネスや実生活の場面で、どのように役に立ってきたのでしょうか。
統計学によって人類の寿命が延びた
「公衆衛生」「社会医学」「保健行政」などの分野では、命の選択にかかわる意思決定が行われています。イギリスでは、産業革命以後に都市部へ人が集まったところで発生したコレラの大流行によって、多くの人が亡くなりました。
研究者のひとりは、コレラが発生した家とその近所の観察を行い、違いを比べました。すると、水道会社によって1万軒あたりの死亡者数が8倍も異なることをつきとめたのです。
異なる水道会社における死亡者数の大小を単純比較するのではなく、同じような家屋の大きさや住んでいる人数をそろえ、1万件あたり、という条件を整えることで発生リスクのある水道会社を特定できました。
研究者の提言によりリスクのある水道会社の使用をやめた地域では、コレラの発生がおさまったといいます。これはコレラ菌が発見されるずいぶん前のことで、議論だけでこのような結果を導くことは不可能でした。
このように、データをもとに統計的分析をすすめる疫学の考え方が広く認識されるようになり、人類の寿命が大きく伸びたのです。
上記の例のように、病気の予防や治療方法を見出すことに統計学を用いることができます。しかし、その他にも経済指標に使われる消費者物価指数や工業統計調査、また経営分野におけるマーケティングや人材マネジメントといった場面でも、統計学的に効果のある手法が明らかになっています。
教育やスポーツといった分野でさえ、成果をあげる仮説を検証するためにデータを取得し、統計的な処理を行うことで、有用性を判断できるようになってきているのです。統計学を使いこなすことができれば、勘や経験をもとにした議論を避け、現時点での最善の答えを明らかにすることができます。
手計算の時代からITを活用した統計学の時代へ
1900年代前半には、今につながる統計学的分析手法は確率されていました。しかし、一般には手計算で分析をすすめなければならない時代でした。パンチカードをつかって入力することができても、その蓄積された大量のデータを処理するためには、コンピューターの登場を待たなければなりません。
時代は進み、現代の先進国では一人ひとりがパソコンを所有できる環境にあります。統計ソフトを活用して、簡単な操作で処理ができるようになりました。
ネットワークインフラも充実し、商品の発注や在庫管理などのビジネスプロセスもIT化され、ログは記録されています。ハードウェアやソフトウェアが発展した今、あらたな価値を生み出そうと、「ビッグデータ」や「AI」「ビジネスインテリジェンス」といった言葉がうまれ、注目されています。
統計学には、大きく6つの分野があります。

統計学はさまざまな分野で応用することが可能ですが、仮定の置き方には独読な考え方があり、細分化が進んでいます。
商業ベースのデータが蓄積され始めたことで、社会調査だけではなく、ビジネスにおける統計学が注目されはじめています。では、ビジネスデータを解析することでどのような価値が生まれるのでしょうか。
電子商取引をしている企業は、コンバージョン(例えば購買率など)を重要視して、ウェブサイトのデザインを変える取り組みを行うことがあります。ボタンの大きさや色などを変えたサイトパターンをいくつか準備し、アクセスに応じてランダムに表示して、よりよい結果をもたらす改善を行います。
一般的に、これらの手法をA/Bテスト(スプリットテスト)と呼びます。
仮に2パターンで比較をした結果、売上に差が生じたとして、「テスト期間中の売上を集計して良い方を選べばいい」という選択をするのは、少々短絡的すぎる意思決定です。
全体のアクセス数に対して、テストを実施したアクセス数が少なければ、誤差が大きくなるものなのです。偶然やたまたまといった差分を除外して意味のある数字として議論するためには、テスト中の売上の差が誤差よりも大きいことを考慮しなければなりません。そのために役立つのが統計学の知識なのです。
今後、統計学を理解できる人材が多く求められる時代になってきます。コンピューター技術が発展した現代において、実際に自ら統計的な計算を行うことは少ないでしょう。
しかし、その理論を理解し、意味ある方向づけができる人材は重宝されるようになります。ビッグデータ時代の21世紀を生きていくためには、ビジネスパーソンが統計学を学ぶことは重要なのです。
統計学はどのようにビジネスに役立つか
それでは、具体的に統計学はどのよにビジネスに役立つのでしょうか。それを理解するために、サンプリングについて考えてみます。
サンプリングが情報コストを激減させる
日本で実施されている最大規模の全数調査は国勢調査ですが、世の中の動きを知るために必ずしも全数調査が必要になるわけではありません。たとえば、選挙時には投票締め切り直後に当落速報が流れますが、これは出口調査の結果によるものです。
抜粋された一部データから導き出された結果が、ある誤差の範囲内に収まることがわかっており、ニュース速報として報道されます。このような調査方法をサンプリングと呼びます。
投票の最終開票結果と速報を照らし合わせてみれば、一部には誤報もあります。しかし、一定数の誤差を許容範囲として、サンプリングから得られた結果はおおむね正しいものであることは多くの人が知るところでしょう。
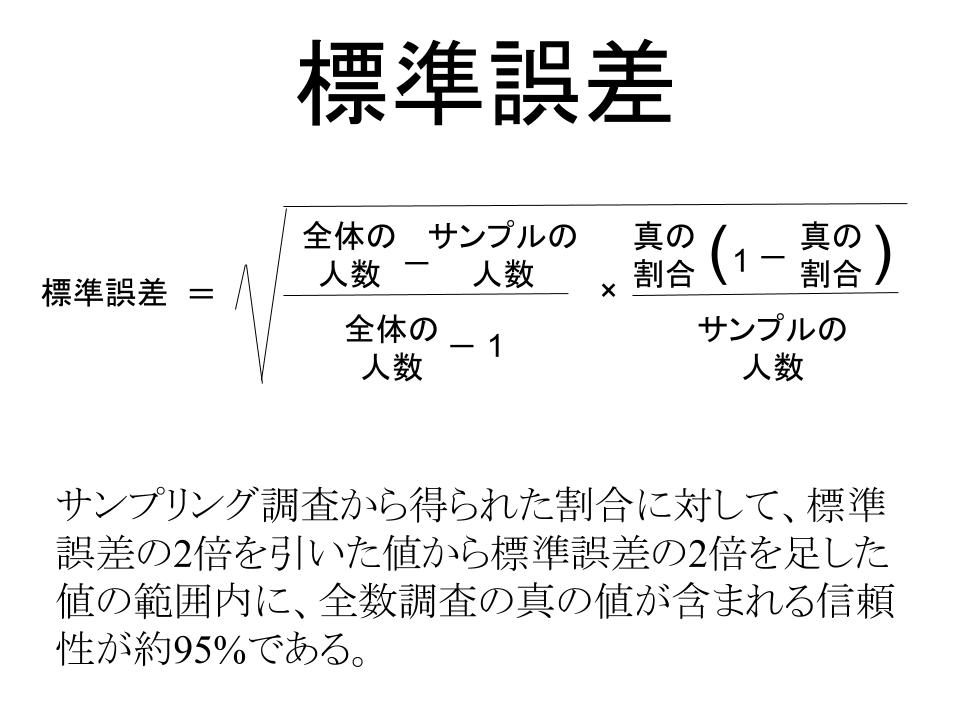
・サンプリング調査から得られた割合に対して、標準誤差の2倍を引いた値から標準誤差の2倍を足した値の範囲内に、全数調査の真の値が含まれる信頼性が約95%である。
あるサンプリング調査から、A社の商品Bをすでに保有している人の割合が全国民の25%で、標準誤差が0.5%であったと仮定します。この場合、全数調査から得られる真の保有割合は、24〜26%の範囲内にほぼあると考えられるということを示しています。
では、どのぐらいのサンプル数を集めればよいのでしょうか。とある商品Xを購入している人の男女比を調べたいとき、販売人数10万人を対象にした場合に女性が70%であると仮定します。
サンプル数が100人の場合、標準誤差は4.6%です。この場合、「女性の割合は、60.8〜79.2%と考えられる」といえます。サンプル数が1,000人の場合、標準誤差は1.4%です。この場合、「女性の割合は、67.2〜72.8%と考えられる」といえます。
さらに、サンプル数が10,000人の場合、標準誤差は0.4%で、この場合、「女性の割合は、69.2〜70.8%と考えられる」となります。
10万人を対象に調査したい場合、100人のサンプリングでは60.8〜79.2%と大きなギャップが生じる可能性があります。しかし、1,000人を超えるあたりからおよそ70%といえる範囲に収まっています。
10万人全数を調査するコスト、10,000人を調査するコスト、1,000人を調査するコストを比較をして、目的に応じた必要最小単位でのデータを分析をすればよいことがわかります。
10,000人分のデータであればハードウェアやソフトウェアに投資することなく、ビジネス用に準備された標準パソコンの表計算ソフトでの分析も可能です。
このように、統計学のサンプリングと標準誤差の知識をもってビジネス分析の範囲を決定することで、ムダな投資をせずにすみます。統計学の知識をもち、単なる集計ではなく、誤差を考慮したうえで意味のある施策をみつけることが重要なのです。
データをビジネスに使うために
データを統計学的な処理をすることで、どのような価値が生まれるのでしょうか。ビジネスの現場であれば、「いかに自社の利益を最大化させるか」に答えることが大事です。
電子商取引の場合、ウェブサイトの認知から会員登録につなげ、ダイレクトにメールでセールを告知すれば、直接的に売上に影響を及ぼしそうなことはわかります。
また、生産設備のログを分析すれば、故障する場合としない場合の差がわかり、メンテナンスコストの削減ができるかもしれません。
まずは、どのようなデータを保持していて、何が売上につながるのか、何がコスト削減につながるのか、それらを導く考え方をクリアにしてみましょう。そのうえで、誤差とは考えにくい「偏り」を発見することができれば、利益を上げる仮説につなげられるのです。
例えば、小麦の生育に有効な農薬を調査する場合、日当たりや水はけといった諸条件をどのように扱えばよいのでしょうか。これは、実験対象となる畑をランダムに選択すれば、諸条件が平均的に同じになるといった状況を生み出すことで解決します。
そのうえで、農薬の有無だけ差をつけて収穫量を比較するのです。ただし、このようなランダム化には限界があります。実験できないような現実の場面では、統計学は役に立ちません。
たとえば、企業買収にかかわる事案や自身の結婚に関することです。次に、有害な結果をもたらすことは倫理的に許されることではありません。最後に、人の感情の反発を意識しなければなりません。顧客により接客対応を変えたことが知られれば、不信感をもたらす可能性があるからです。
このようなことに注意しながら、統計学をビジネスに活かしていきましょう。
