男女の争いとチキンゲーム

トップページ＞ゲーム理論＞男女の争いとチキンゲーム

ゲーム理論のモデルの中には「男女の争い」と呼ばれるモデルがあります。

このモデルの特徴は、プレイヤーである男と女にとって同じ戦略を選ぶことが互いの利得を大きくするという点と、どちらにとっても利得が大きくなるナッシュ均衡がなく、プレイヤー間で争いが起きる点です。

前者に関してはコーディネーションゲームと類似していますが、後者に関しては対立の要素を含んでいます。「男女の争い」は協調と対立、両方の要素を含むモデルなのです。では具体例を見ながら、このモデルについての理解を深めましょう。

AとBはカップルです。2人は毎週木曜日に次の週末の予定を決める時間を設けていましたが、Aは「山登りを提案しよう」と考えており、Bは「美術館を提案しよう」と考えています。

2人で過ごすことが前提なので、1人で山に登っても、あるいは1人で美術館に行ってもちっとも楽しくありません。しかしやはりAは「山が1番楽しい」と考え、Bは「美術館が最高だ」と考えています。

この状況の利得表が下図です。「2人で過ごせる」という点で、Aが美術館に、Bが山に行ってもそれなりに楽しめますが、やはり希望の場所に行ける方が利得が大きくなります。そのためいくら話し合いをしてもこのモデルにおける「対立」の要素はなくなりません。

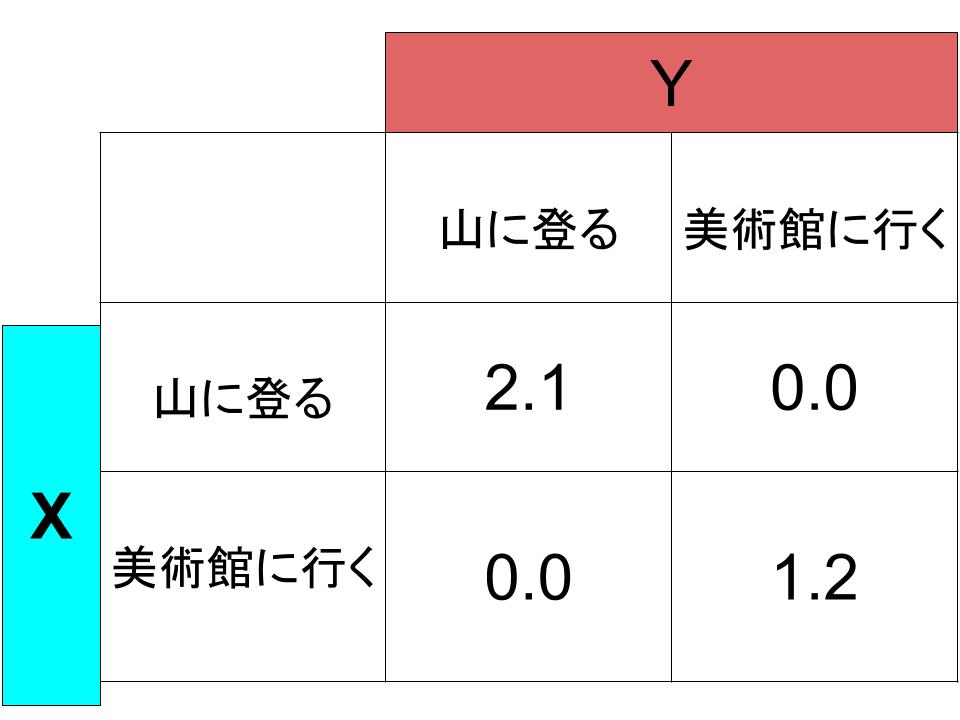
男女の争い

またこの利得表だけで考えれば、どちらか一方が「何が何でも山（あるいは美術館）に行くんだ！」と言って、自分の行きたい場所に行ってしまうと、もう一方は利得がゼロになってしまうために、その強硬策に従わなければならなくなります。

「2人で過ごすことが前提」であるばかりに、押しの強い方が決裁権を持ってしまうのです。

次にチキンゲームというモデルを見てみましょう。戦略が協調することが好ましいコーディネーションゲームや、「男女の争い」などと異なり、「チキンゲーム」モデルは対立することこそが最善です。

このモデルは交渉が必要な局面に当てはまることが多いとされています。具体的な例を見て、理解を深めておきましょう。

暴走族Pと暴走族Qが下っ端同士の鍔迫り合いから泥沼の抗争に発展し、このままでは収拾がつかないと判断したリーダー同士が話し合い、2人のチキンゲームで決着をつけることにしました。

一直線の道路の端と端にバイクを停め、スタートの合図で全速力で走り出し、互いに向かって正面から突進するゲームです。先にハンドルを切って避けた方がチキン=臆病者とされ、今後相手の暴走族の傘下に入らなくてはなりません。

そのまま直進し続けた場合は「腹が据わっている」と賞賛され、暴走族PとQの連合リーダーになれますが、もし両方が直進し続けた場合は間違いなく命を落としてしまいます。

両方が同時に避けた場合は、今回の抗争を2人のリーダーの引退で手打ちにするということが、双方の幹部会で取り決められました。

この状況を利得表にすると下図のようになります。純粋戦略（図1）で考えた場合、PとQが互いに違う戦略を選んだ場合にナッシュ均衡となるため、ナッシュ均衡は2つです。混合戦略（図2）で考えた場合は、互いに直進を1/7、避けるを6/7で選ぶ場合にナッシュ均衡となります。

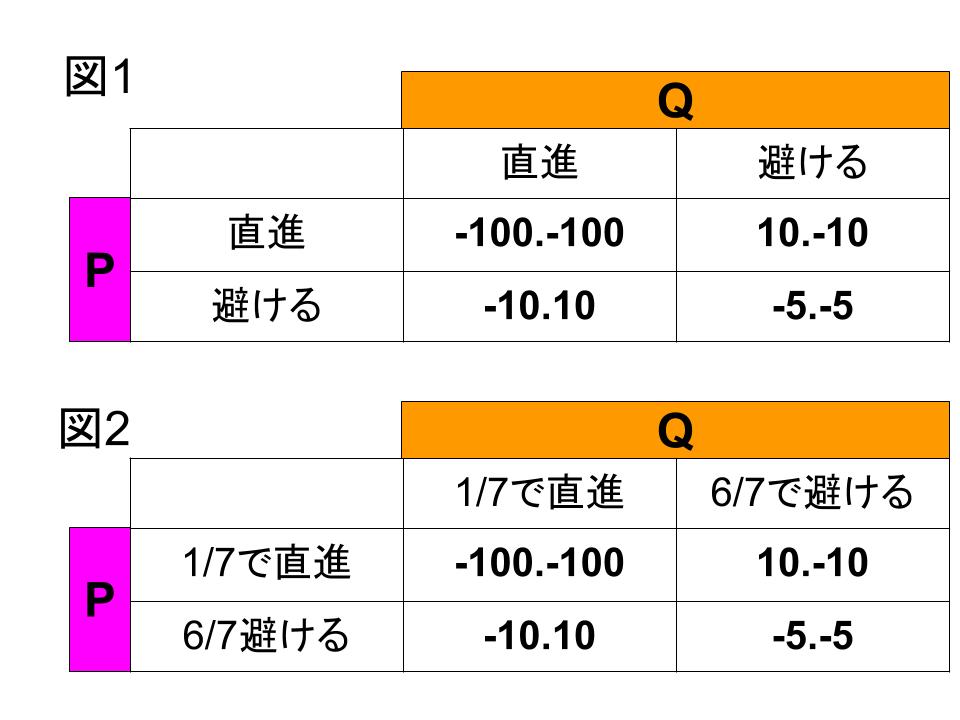
チキンゲーム

・Pが直進した場合
期待利得=1/7×（?100）＋1/7×10=?90/7

・Pが避けた場合
期待利得=6/7×（?10）＋6/7×（?5）=?90/7

※Qの計算式はPのものと同じ

このモデルのポイントは「強硬姿勢」を選ぶか、「譲歩」を選ぶかです。相手が譲歩を選ばなければ得はしませんが、かと言って相手の強硬姿勢に対して、自分も強硬姿勢をとり続ければ最悪の結果が待っています。

交渉に置き換えて考えると、交渉の決裂が「最悪の結果」であり、相手に譲歩させてこちらに有利な条件をいかに飲ませるかが勝負になるというわけです。

・「男女の争い」は協調と対立、両方の要素を含む

・「男女の争い」は先に戦略を選んだ方が決裁権を持つことになる

・「チキンゲーム」は「強硬姿勢」を選ぶか、「譲歩」を選ぶかがポイント

・交渉の場面はこの「チキンゲーム」モデルが当てはまりやすい

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど