ナッシュ均衡を理解する
ゲーム理論を理解する上で「ナッシュ均衡」は非常に重要な解の概念です。
ナッシュ均衡とは「すべてのプレイヤーが互いに最適な戦略を選択している状態」を指します。
この「最適な戦略」とは「自分の利得が最も大きくなる戦略」であり、ゲーム理論では「最適反応」と呼びます。つまり、全プレイヤーが最適反応を選択している状態がナッシュ均衡です。
アメリカの数学者ジョン・フォーブス・ナッシュ・ジュニアによって証明されたことにちなんでこの名前が付けられました。
「囚人のジレンマ」や「合理的な豚」など数多くのモデルでもこのナッシュ均衡は登場しています。
ナッシュ均衡はゲームの安定状態を作る
ナッシュ均衡は言い換えれば「ベストな状態」です。
プレイヤーは一度最適反応を選択すると、それ以外の戦略を選ばなくなります。そのためゲーム的状況にナッシュ均衡が実現されると、ゲームは安定状態に入ります。
逆にゲーム的状況がナッシュ均衡でない場合とはプレイヤーのうちの誰かが最適反応を選べていないということです。
プレイヤーが合理的である、つまり自分の利得が最大になるように行動する場合、最適反応を選べていないプレイヤーは最適反応を選ぶために戦略を変更します。これは「誰も戦略を変更しない」=「ナッシュ均衡である」ということでもあります。
例題1
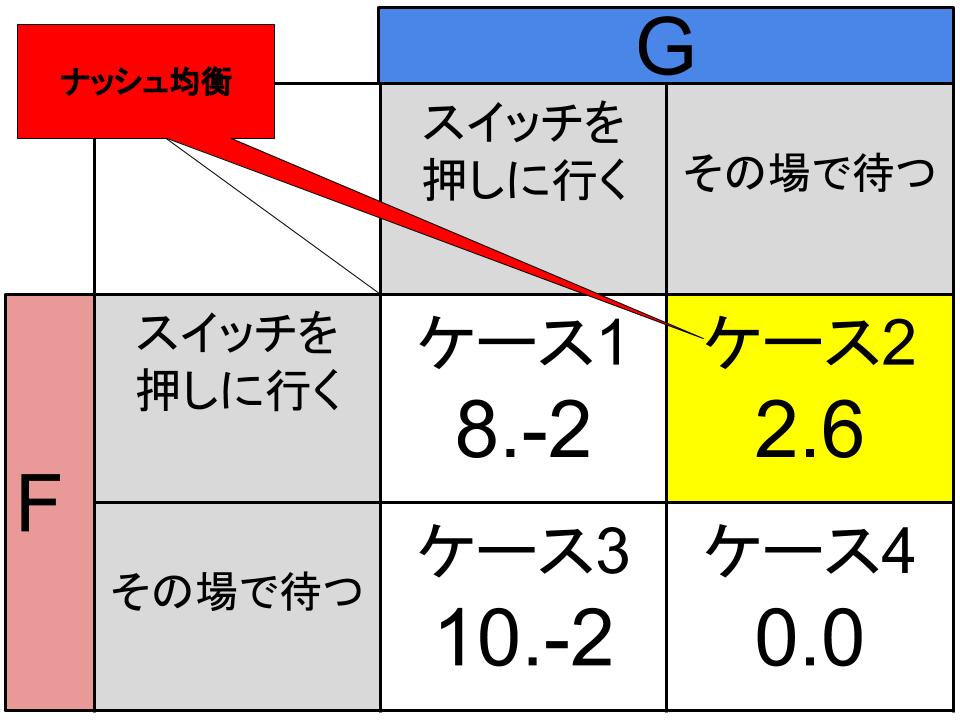
支配戦略のところで説明した、豚Fと豚Gをプレイヤーとして成立する「合理的な豚」モデルが下図のような利得表を構成するとします。この場合のナッシュ均衡について考えましょう。
解説
まず豚Fの最適反応について考えます。豚Gが「スイッチを押しに行く」を選択した場合の豚Fの最適反応は「その場で待つ」です。
逆に豚Gが「その場で待つ」を選択した場合、豚Fはスイッチを押しに行かなくては利得を得ることができないので、豚Fの最適反応は「スイッチを押しに行く」になります。
豚Gにとっては豚Fがどのような戦略をとっても「その場で待つ」が最適反応(と同時に支配戦略)です。
2匹の豚が最適反応を選択しているの場合では、豚Fが「スイッチを押しに行く」を選び、豚Gが「その場で待つ」を選択している、すなわちケース2がナッシュ均衡となります。
複数のナッシュ均衡がある場合もある
ナッシュ均衡は常に1つだけとは限りません。1つのゲームの中に複数のナッシュ均衡が存在する場合もあります。このようなとき、どちらのどのナッシュ均衡が選ばれるかは理論的には説明できません。例えばそれは慣習であったり、偶然であったりします。
以下ではこの場合について例を見ておきましょう。
例題2
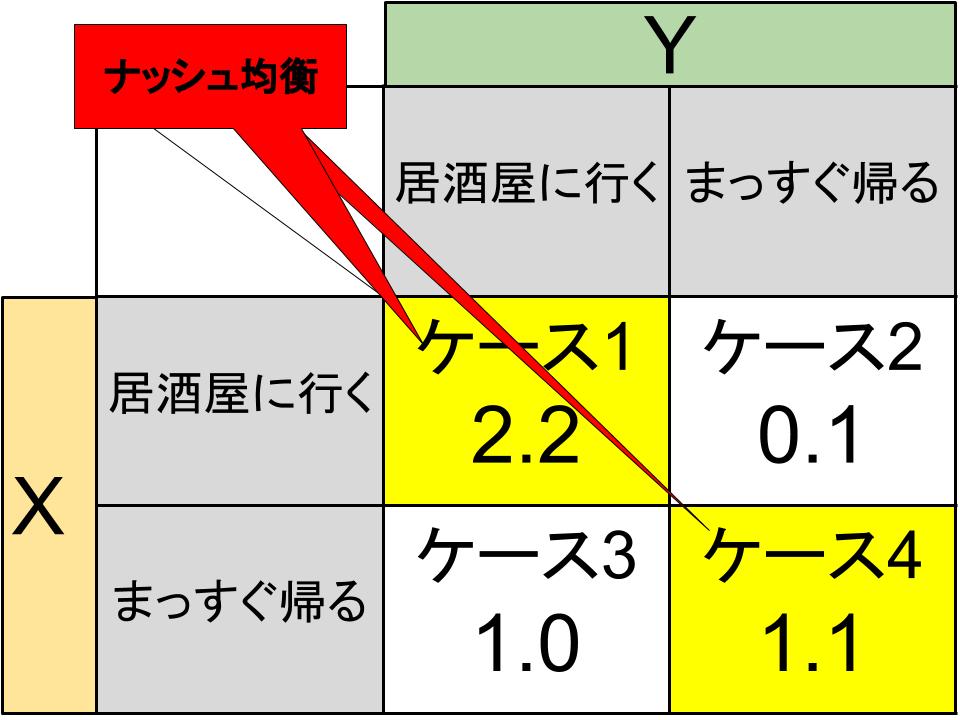
同期の会社員XとYをプレイヤーとする「居酒屋ゲーム」モデルが下図のような利得表を構成するとします。この場合のナッシュ均衡について考えましょう。
解説
居酒屋ゲームにおいては「相手が居酒屋に飲みに行くのであれば自分も行きたい」と「相手が飲みに行かないのであれば自分はまっすぐ家に帰る」という、相手の戦略に依存した意思決定が行われます。
これは「支配戦略」の観点から見ると「支配戦略のないゲーム」とされるモデルです。
しかしナッシュ均衡について考えるとき、このモデルは複数のナッシュ均衡を持つモデルとして考えることができます。
仮にXが「居酒屋に行く」と決めればYの最適反応は「居酒屋に行く」です。Yが「居酒屋に行く」場合のXの最適反応も「居酒屋に行く」なのでケース1はナッシュ均衡です。
Xが「家に帰る」と決めたときのYの最適反応は「家に帰る」となります。Yが「家に帰る」ときのXの最適反応も「家に帰る」なので、ケース4もナッシュ均衡です。よって「居酒屋ゲーム」は複数のナッシュ均衡を持つモデルと言えます。
ナッシュ均衡の見つけ方
ゲームのプレイヤーが全員最適反応を選んでいる「ナッシュ均衡」は、ゲーム理論における解の最も重要な考え方の1つです。
ナッシュ均衡を効率的に見つけるために役立つのが「利得表」。表の中に印をつけていくだけで簡単にナッシュ均衡を見つけることができます。
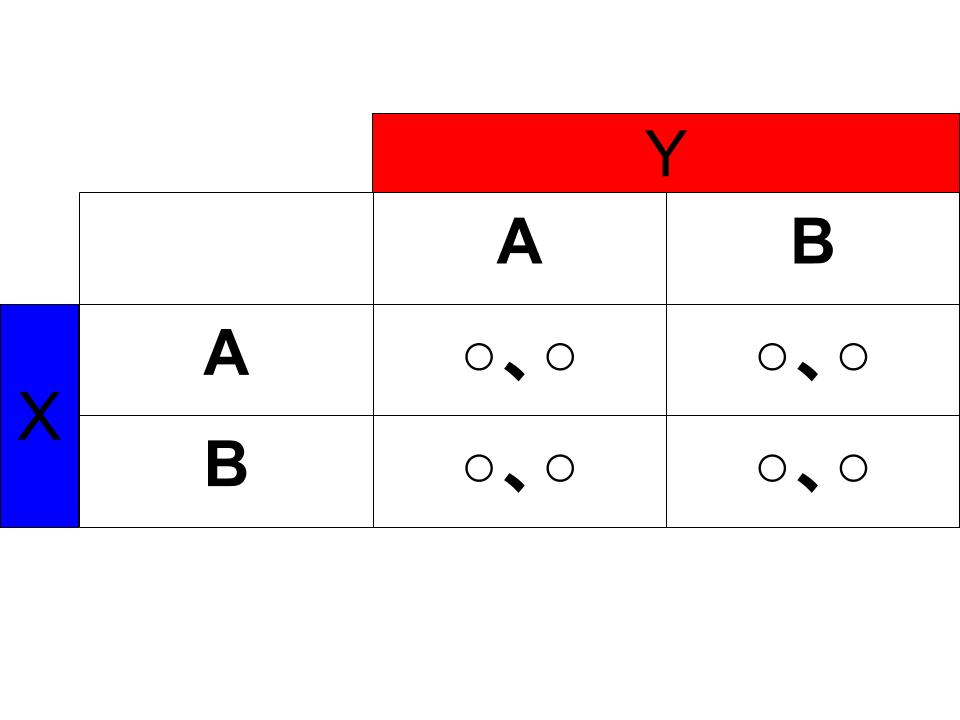
2人のプレイヤーがいる場合、まずはXの最適反応をYのそれぞれの戦略に対して考え、その利得に対して「○」をつけていきます。
これと同じようにYの最適反応に対応する利得についても「○」をつけましょう。この時、両プレイヤーの利得に「○」がついている戦略が、このゲームにおけるナッシュ均衡となります。
ではゲーム理論のモデルを使って、それぞれのナッシュ均衡を探してみましょう。
例題-合理的な豚
食べる速度も歩く速度も速い豚Pと、食べる速度も歩く速度も遅い豚Qが、離れた場所にあるスイッチを押すと開くエサ箱の前にいます。
両方の豚がスイッチを押しに行くと、先にエサ箱にたどり着いた豚Pがたくさん食べてしまい、豚Qは少ししかエサを食べられません。豚Pがスイッチを押しに行くと、豚Qは先ほどよりは多くのエサが食べられますが、やはり食べるのが遅いので帰って来た豚Pに残りを食べられてしまいます。
逆に豚Qがスイッチを押しに行くと、エサ箱の前に到着した頃には豚Pが全てのエサを食べつくしてしまうので、豚Qは体力を消耗しただけで一切エサが食べられません。両方の豚がスイッチを押さなければ、エサ箱は開かず、二匹ともエサを一口も食べられません。
解説
この状況を利得表にしたのが下図です。この表に先ほどの手順に従って「○」をつけていきましょう。
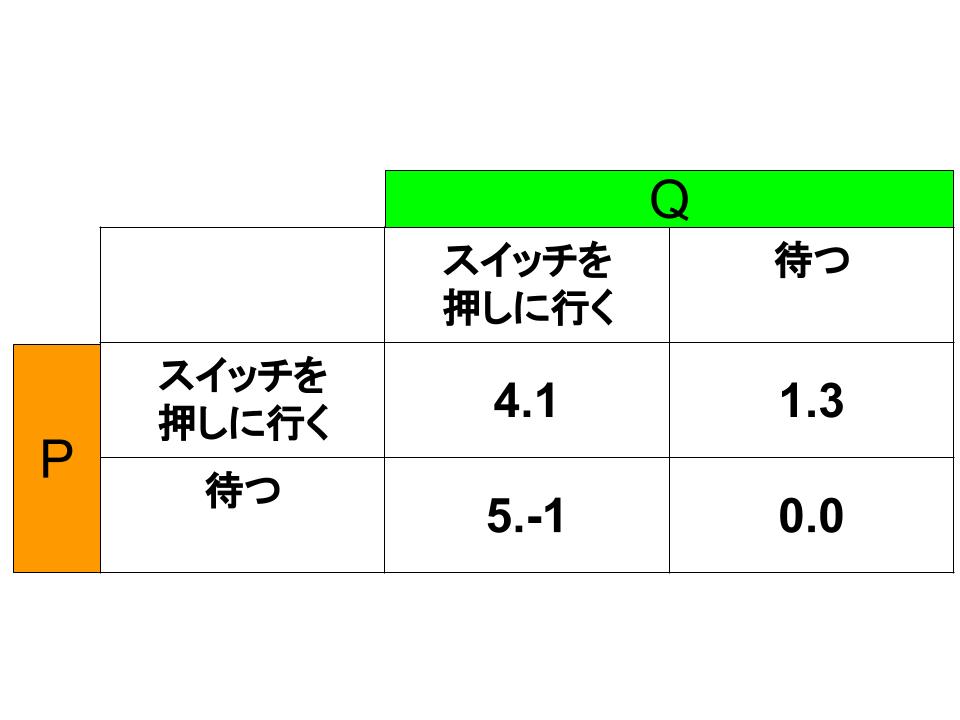
まず豚Pにとっての最適反応を考えます。豚Qがスイッチを押しに行ったときの豚Pの最適反応は「その場で待つ」です。対して豚Qがその場で待っているときの豚Pの最適反応は「スイッチを押しに行く」。
では豚Qの最適反応はどうでしょうか。豚Pがスイッチを押しに行ったときの豚Qの最適反応は「その場で待つ」です。豚Pがその場で待つときの豚Qの最適反応も「その場で待つ」。それぞれに対応する利得に「○」をつけたのが下図です。
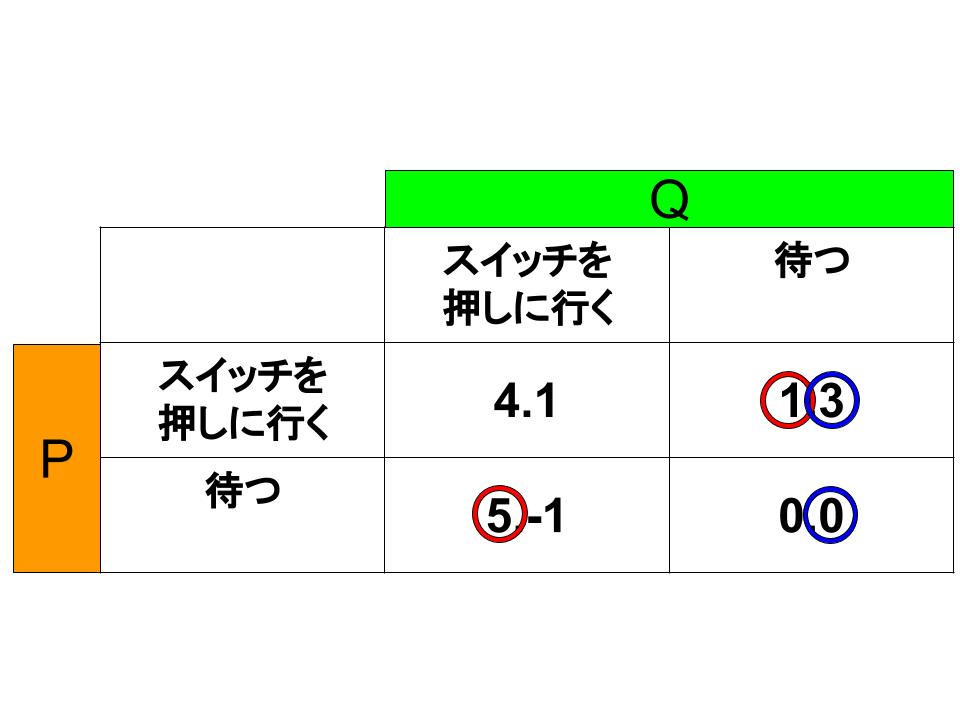
結論として、豚Pがスイッチを押しに行き、豚Qがその場で待つのがこのゲーム的状況のナッシュ均衡ということがわかります。
例題-取り調べゲーム
FとGは協力して大富豪の家に泥棒に入り、見事金品を盗むことに成功します。2人の盗みは完璧でしたが、FとGの仕業だと確信した警察は、別件の傷害容疑で2人を逮捕し、別々の取調室で尋問することにしました。
FとGは1人1人が超一流の泥棒だったので、窃盗の証拠はありません。しかし1人でも野放しにすれば、また盗みを働くことはわかっています。取調をする検事は何としても両方を刑務所に入れたいと考えました。
そして担当刑事などと相談した結果「今回は司法取引なしで取り調べを行う」という方針を固めます。
もし2人ともが黙秘を決め込んだ場合には傷害罪で2人とも3年の服役。どちらかが自白したり、両方が自白した場合は2人とも9年の服役です。
解説
この状況を利得表にしたのが下図です。ではそれぞれの最適反応を見ていきましょう。
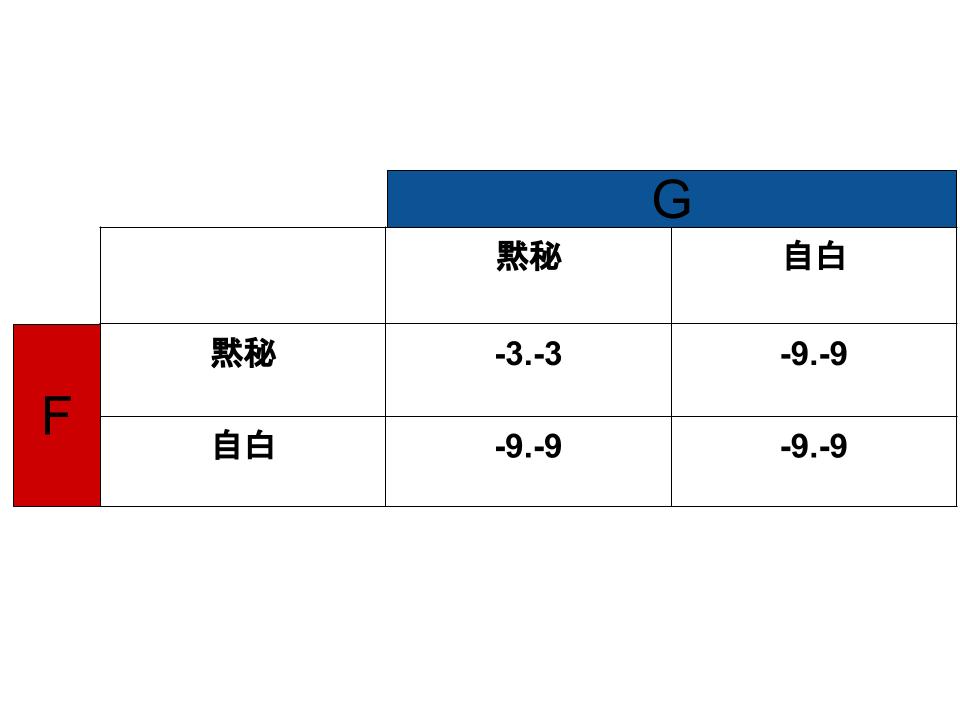
Gが黙秘した場合のFの最適反応は「黙秘」です。対してGが自白すれば、Fの利得は「黙秘」しても「自白」しても変わりません。
これはGの最適反応についても同じです。Fが黙秘すればGは「黙秘」、Fが自白すれば「黙秘」「自白」どちらを選んでもGの利得は変わりません。
それぞれの最適反応に対応する利得に「○」をつけると下図のようになります。
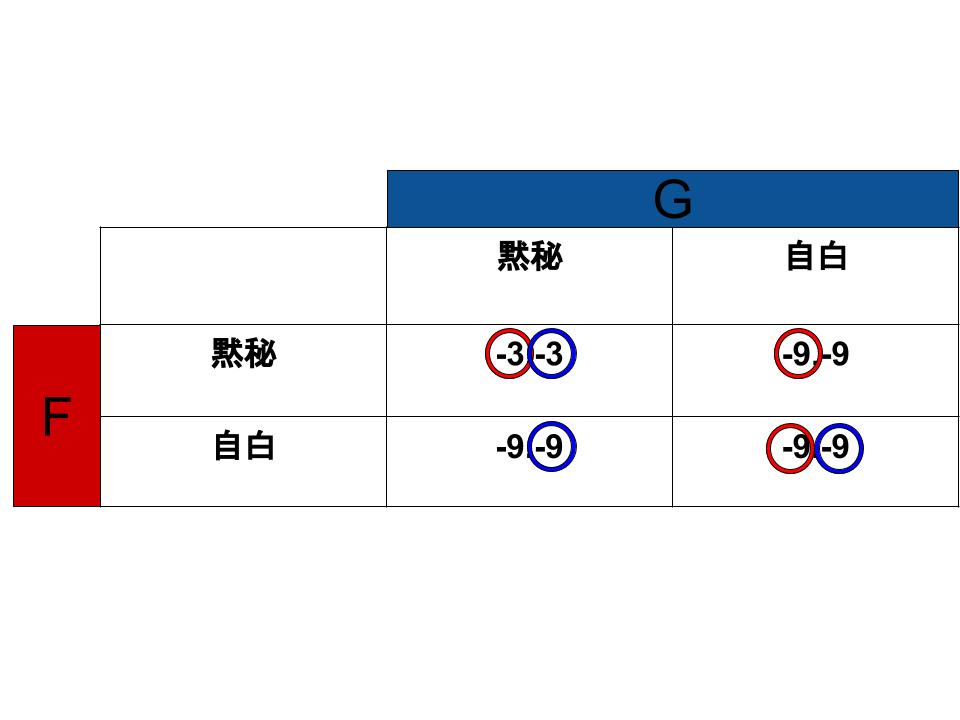
「司法取引をしない」というルールのもとで行われるこのゲームの解は「両方とも黙秘する」になります。なぜならそれが2人にとって互いに最も大きな利得につながるからです。
FとGがもう一方のナッシュ均衡「両方とも自白する」を選ぶのは、例えばFとGが「これまでの泥棒の仕事に少なからず罪悪感を感じていて、後悔もあり、今回の仕事を最後に泥棒業から足を洗おうと話し合っていた」といった場合。
これは「きっと相手は自白するだろうから、自分は黙秘しても自白しても同じだが、どうせなら自白しておこう」と考えている状態です。
複数のナッシュ均衡がある場合、プレイヤーたちがどちらのナッシュ均衡を選ぶのかは、論理的に説明はできません。
まとめ
・ナッシュ均衡=すべてのプレイヤーが互いに最適な戦略を選択している状態
・最適反応=自分の利得が最も大きくなる戦略
・ナッシュ均衡=ゲームの安定状態(誰も戦略を変更しない)
・ナッシュ均衡が複数あるゲームもある
・ナッシュ均衡が複数ある場合、どのナッシュ均衡が選ばれるかは理論的に説明できない
・各プレイヤーが相手の各戦略に示す最適反応に対応する利得に「○」をつけて、両方の利得に「○」がついた戦略の組み合わせがナッシュ均衡になる
関連ページ
- ゲーム理論とは…意味を理解してビジネスの駆け引きの現場で活かす
- 交互進行ゲーム(逐次手番ゲーム)とゲームの木
- ゲーム理論の視点からオークションの仕組みを理解する
- ベイズ均衡(ベイジアンナッシュ均衡)
- 男女の争いとチキンゲーム
- コーディネーションゲーム(失敗と解決法)
- クールノー競争とベルトラン競争
- ゲーム理論の基本を理解する(囚人のジレンマ)
- ホテリングの立地ゲーム
- 情報非対称ゲーム(不完備情報のゲーム)
- ミニマックス定理
- 混合戦略と純粋戦略
- ナッシュ均衡を理解する
- 部分ゲーム完全均衡と後ろ向き帰納法
- 囚人のジレンマの解決法
- 戦略形ゲームのモデルを理解する
- 脅しのゲームと信頼のゲーム
- 交互進行ゲームにおける戦略と信頼性のない脅し
