囚人のジレンマの解決法

トップページ＞ゲーム理論＞囚人のジレンマの解決法

別々の取調室で司法取引を持ちかけられた2人の囚人は、本来であれば2人とも黙秘を続けるのが最善策であるにもかかわらず、ゲーム理論に基づいた意思決定を行うと2人とも自白をしてしまう。これが「囚人のジレンマ」です。

このジレンマが起きる原因は、相手が自白する危険性があるから。「相手が自白するかもしれない」と思うからこそ、自分だけ黙秘を続けることで重い刑罰を受ける危険を回避するために、相手が自白しようが黙秘しようが自分にとっての利得を確保できる「自白」を選ぶのです。

囚人のジレンマを解決するにはどうすればいいのでしょうか。答えは簡単。「相手が自白する危険性」をあらかじめ排除しておけばいいのです。

例えば「もし司法取引を持ちかけられたら、必ず黙秘すること」と契約を交わしておく。こうすれば「もしかしたら相手が自分を売るかもしれない」という不安を軽減できます。

しかし相手との関係性によっては、単に契約するだけでは相手が契約を破る可能性を捨てきれません。

そこで自白した場合の罰則事項を設けるなどして、より契約に拘束力を持たせる必要があります。このような方法は実社会でもいくつか見つけることができるので、以下で2つの例を見ておきましょう。

X社とY社が同一市場で全く均質な財を販売しています。ある時X社の社長が「これからは安売りの時代だ！」と言い出し、自社製品の値下げを突然断行しました。

ベルトラン競争のところでも見たように、こうなると消費者はY社製品を全く購入しなくなり、X社に完全にシェアを奪われてしまいます。したがってY社はX社よりも低い価格をつけようとするでしょう。

結果2社は値下げ競争を展開し、利潤をどんどん削っていくことになります。

下図はX社とY社が陥っている「囚人のジレンマ」的状況を図示したものです。両社とも本当は利潤を最大化したいにも関わらず、相手が値下げをするのに対抗してどんどん利潤を最小化させていきます。

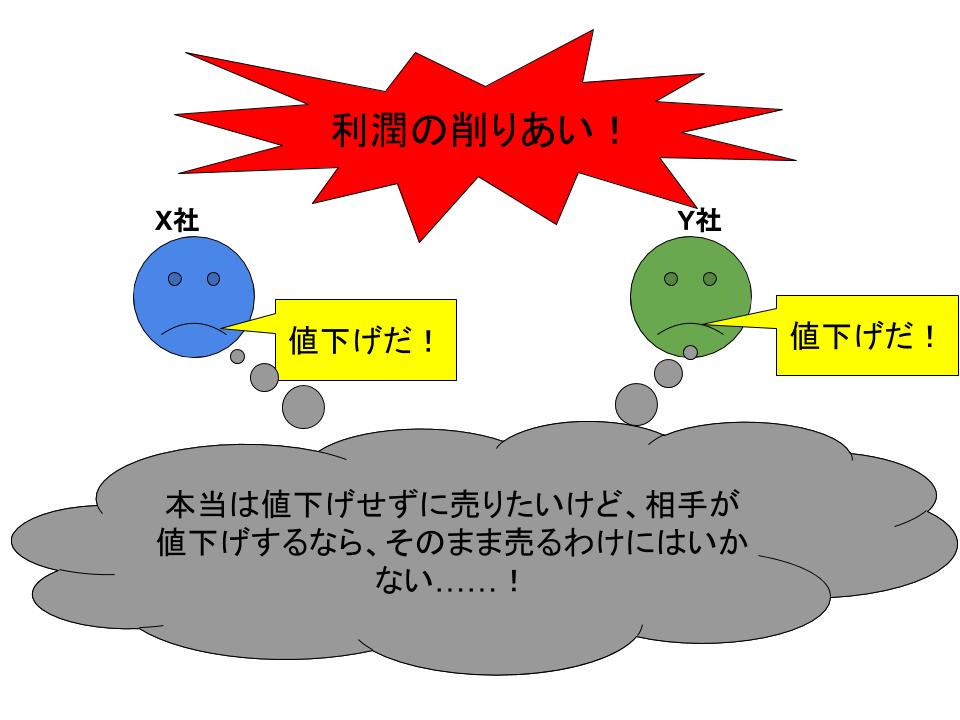
囚人のジレンマの解決法

この状況を解決するには「○○円以下の価格で販売した場合には契約違反として罰金××円を申し受ける」などの罰則事項とともに、契約を結んでしまえばいいのです（法律的問題はここでは考慮しません）。

これにより2社は利益の削りあいをしなくて済みます。

採用活動を行う「企業」と就職活動を行う「学生」の「新卒採用活動時期」をめぐるゲーム的状況を考えてみましょう。

企業としてはできるだけ優秀な人材を確保したいと考えているものの、採用時期が早期化することによりじっくりと就職活動をしていない学生を採用してしまい、結果、人材が定着しないなどの問題が深刻化しているとします。

対して学生側としてはできるだけ早く優良企業に採用されたいと考えているものの、採用時期の早期化は貴重な学生の時間を削ると同時に、じっくりと企業選びができないという問題を招くでしょう。

下図は「企業」と「学生」の「囚人のジレンマ」的状況です。この状況を解決するためには採用時期に制限を設けるとともに、それを破ることについての罰則事項を設ける必要があります。

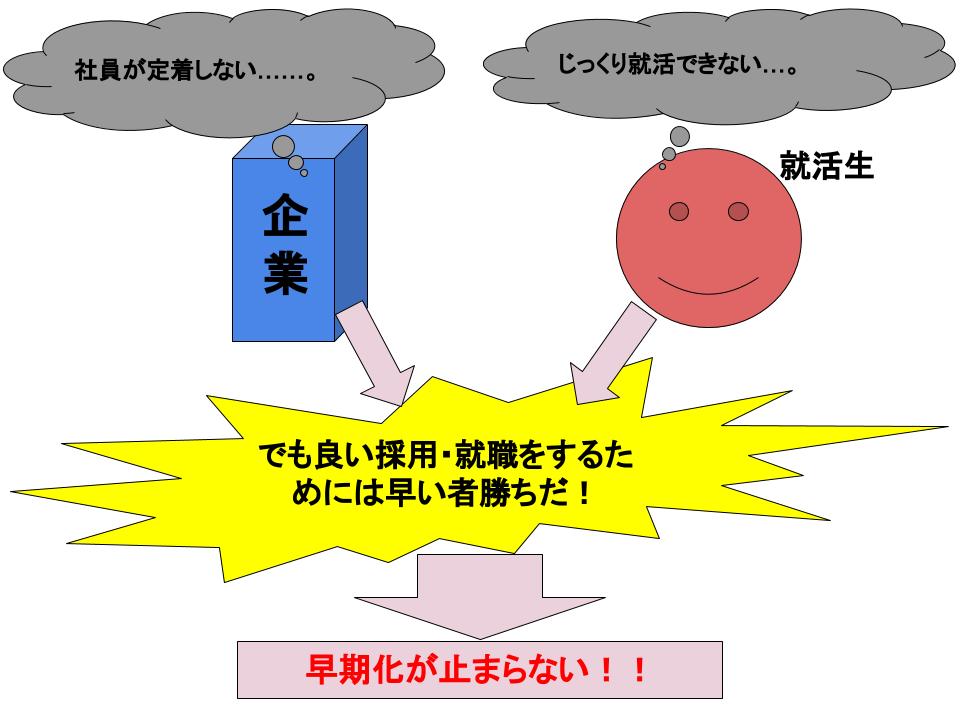
囚人のジレンマの解決法2

採用時期に制限をつける「就職協定」は存在しても、これを破ることについての罰則が設けられていなければ効果が薄くなります。そのため早期化への効果的な歯止めとなるには、罰則を設けることも考慮しなければなりません。

例題1で見たようなX社とY社による「囚人のジレンマ」の解決方法は、現在の日本では独占禁止法で禁止されている行為です。確かに前述の方法であればX社とY社の利潤は確保できますが、消費者にとっては価格が高止まりしてしまうため、大きな損失になります。

したがって例題1の解決方法は法的には妥当ではありません。

対して例題2の採用・就職活動をめぐる「囚人のジレンマ」的状況は、効果的な解決策が打たれておらず、結局状況を解決できていません。

囚人のジレンマを解決するためには「契約」とその拘束力を高める「罰則事項」の2つが重要なのです。

・「囚人のジレンマ」の原因となる戦略を選ばないようにすれば、状況は解決できる

・「囚人のジレンマ」を解決するのは「契約」と、その拘束力を高める「罰則事項」が必要

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど