交互進行ゲームにおける戦略と信頼性のない脅し

トップページ＞ゲーム理論＞交互進行ゲームにおける戦略と信頼性のない脅し

「ゲームの木」のところでも見たように、交互進行ゲームはゲームの木を用いれば相手の出方を見て自分の戦略を選ぶことができます。これをさらにゲーム理論的に考えるために使うのが「ナッシュ均衡」です。

交互進行ゲームでナッシュ均衡を考える場合は、ゲームが開始したと同時にプレイヤーがそれぞれの戦略を決定する「同時進行ゲーム」として整理し直す必要があります。以下で例を用いてこの方法を実際に見てみましょう。

まずは「交互進行ゲーム（逐次手番ゲーム）」で見たケーキショップの例で考えてみましょう。

ある商店街に唯一残るケーキショップXは、その一帯のケーキ需要を独占していました。しかしある時、低価格で有名な隣町のケーキショップYが商店街に出店するかを検討している、という情報が流れてきます。

Xが取り得る戦略は「高級路線に切り替える」か「低価格路線を打ち出す」かの2つだとしましょう。

Yが商店街に出店しない場合にはXが商店街のケーキ需要を独占し続け、Yが出店しXが「高級路線に切り替える」を選んだ場合には利益を半分ずつに分け合い、Xが「低価格路線を打ち出す」を選ぶと、互いに消耗しあって損失を出すと仮定します。

Yには2つのパス、Xには4つのパスがあるため、このゲームを同時進行ゲームに整理し直す場合、Yは2つの戦略、Xには4つの戦略があると考えます。これをもとに作成した利得表が下図です。

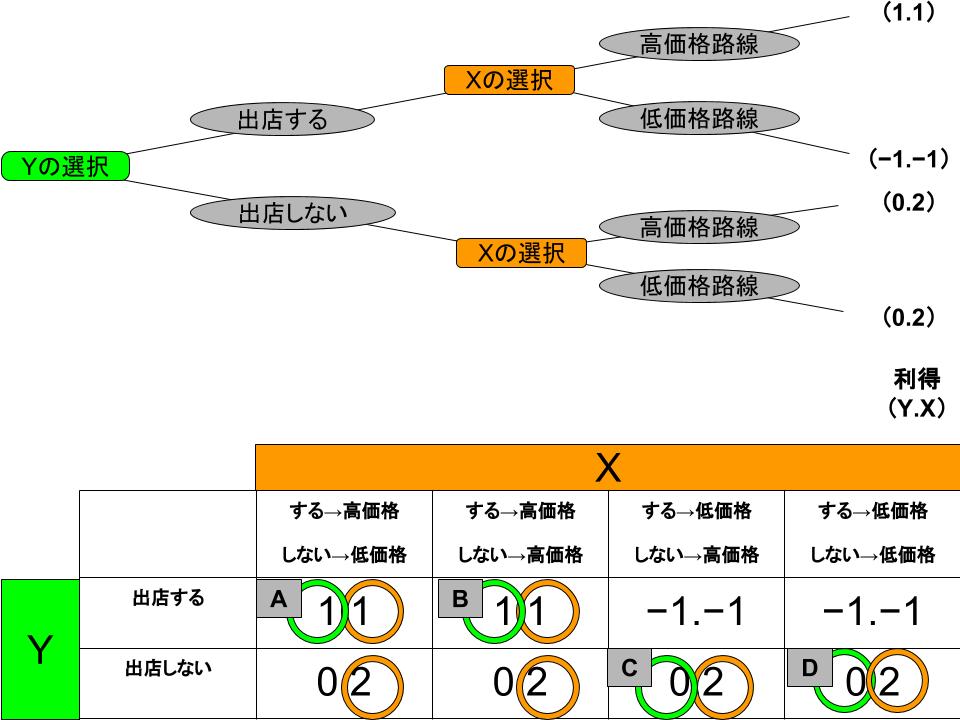
交互進行ゲームにおける戦略と信頼性のない脅し

Yの戦略は「出店する」「出店しない」の2つ。Xの戦略は以下の4つです。

・「Yが出店するなら高価格路線、出店しないなら低価格路線」
・「Yが出店するなら高価格路線、出店しなくても高価格路線」
・「Yが出店するなら低価格路線、出店しないなら高価格路線」
・「Yが出店するなら低価格路線、出店しなくても低価格路線」

Xの戦略は「Yが出店するなら高価格路線or低価格路線」と「Yが出店しないなら高価格路線or低価格路線」の順列組み合わせだと考えればわかりやすいかと思います。この利得表を使って、それぞれの最適反応を記したものが表の中の○です。

この場合のナッシュ均衡は4つ存在します。AとBはYが商店街に出店した場合の利得関係であり、この時のXの戦略はYが出店をしなかった場合の戦略が違うだけなので、利得が一致します。

CとDの場合はYが出店しなかった場合のXの戦略は違いますが、利得は同じ。したがって両方の場合にナッシュ均衡が成立します。

AとBの場合に両プレイヤーが選択するのはYが出店、Xが高価格路線です。CとDの場合にはYは出店しないことを選び、Xはどちらでも好みの方を選ぶことができます。

利得表を見ると、Yは出店しなければどのような場合でも利得は0です。にもかかわらずなぜYが出店しない可能性があるのでしょうか。それはXが低価格路線を選ぶ可能性を考慮しているからです。

例えばXがYに対して「お前の店がうちの商店街に出店したら、低価格路線をとるぞ」と脅しをかけ、Yが自分の店の利得がマイナスになることを恐れて出店を断念した場合です。

しかしYはその脅しに屈する必要がありません。なぜならばYが出店し、Xが低価格路線をとれば、Xも一緒に損をするからです。Xが合理的な人間であれば、利得を最大化するために高価格路線をとらざるをえません。

したがって例題のようなゲームは、実際には「Yが出店し、Xが高級路線をとる」（A・B）という結果に行き着きます。

交互進行ゲームをナッシュ均衡で考えると、このような「信頼性のない脅し」を排除できません。これを排除するためには「部分ゲーム完全均衡」について理解する必要があります。

・交互進行ゲームをナッシュ均衡で考えるときは、同時進行ゲームに整理し直す必要がある

・交互進行ゲームをナッシュ均衡で考えると「信頼性のない脅し」を排除できない

・「信頼性のない脅し」を排除するためには「部分ゲーム完全均衡」について理解する必要がある

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど