ホテリングの立地ゲーム

トップページ＞ゲーム理論＞ホテリングの立地ゲーム

アメリカの経済学者・統計学者のハロルド・ホテリングは、1929年に発表した論文の中に「地理的立地」の問題を取り上げています。

彼はこの問題の考察を通じて、「同じ商圏で全く同じ品質の同じ価格の製品を販売する2つの商店は、最終的に近接した場所に出店する」という「ホテリングの法則」を発見しました。

ここではこのホテリングの法則について解説するとともに、この法則の日常的な例についても紹介します。

焼きそば店を経営するXとYがいます。夏が来たので、今年も近くのビーチに臨時店舗を出そうと考えた2人。どの場所に出店すれば一番儲かるか、それが問題です。

両者の焼きそばは味も全く同じで、価格も全く同じ。差別化できるのは出店場所くらいなのです。彼らは一体どの場所に出店するのが良いのでしょうか。

前提としてビーチの海水浴客はどの場所にも均一にいるとし、かつ自分たちにより近い焼きそば店を利用するとします。

ホテリングが前述の論文の結論として提出したのは下の図1の立地です。

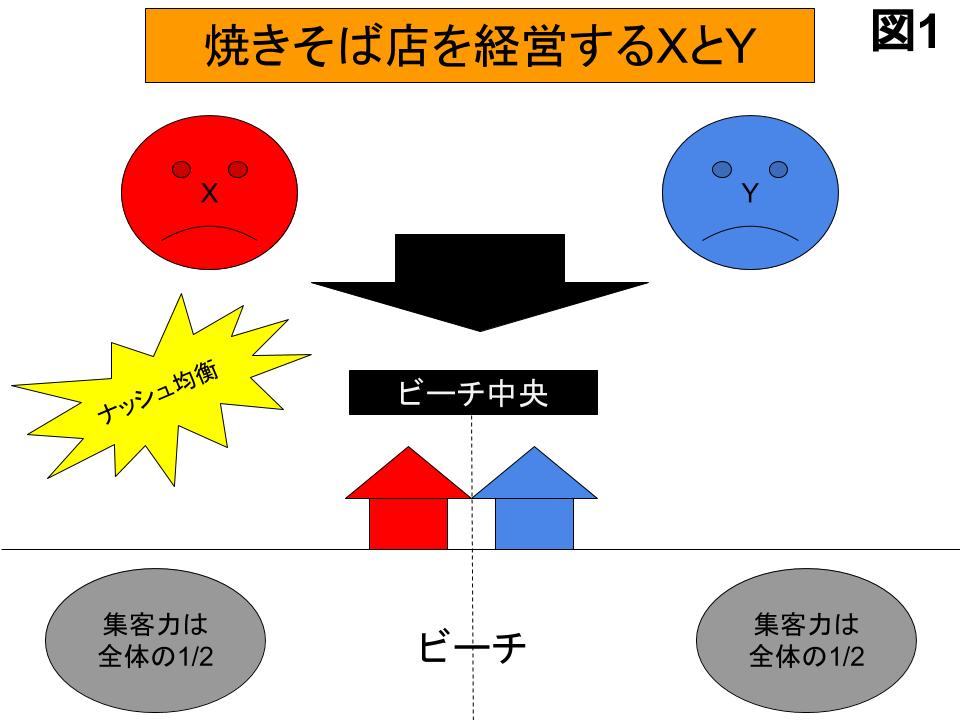
ホテリングの立地ゲーム

ビーチの中央に隣接して出店すれば、お互いの集客はちょうど半分ずつになります。ホテリングによればこれが両者が互いの利益最大化を考えた場合に導き出す結論、ゲーム理論で言えば「ナッシュ均衡」なのです。

しかし商売人なら「相手よりもっと儲けたい」と思うはず。これ以外に選択肢はないのでしょうか。

「XとYがビーチの中央で隣接して出店する」がナッシュ均衡かを確かめるために、下の図2と図3について検証してみましょう。

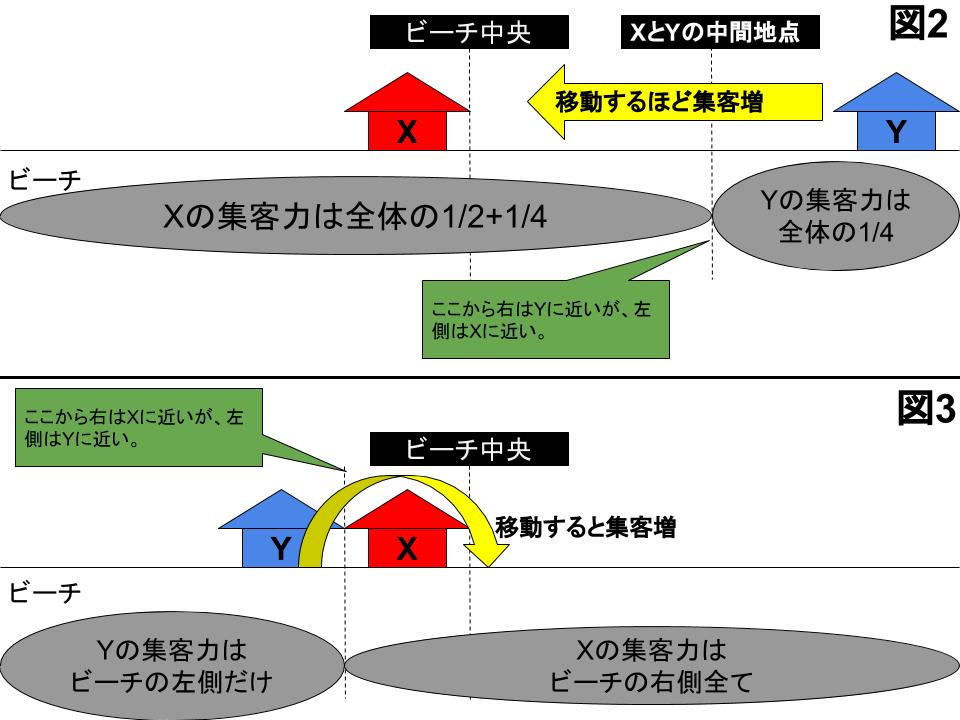
ホテリングの立地ゲーム2

図2は「Xと隣り合って仲良く商売なんてやってられん！」と言って、Xがビーチの中央に、Yがビーチの右端に出店した場合です。この場合の集客力はXの方が高くなります。なぜならば「Xの店に近い海水浴客」が多くなるからです。

対してYの集客力は図1の場合の1/2になってしまいます。

これはYがビーチの中央（Xの焼きそば店）に近寄るほど、Yの集客力が増加していく状況です。ナッシュ均衡の定義は「どちらのプレイヤーも自分だけ行動を変えても得をしない状況」でした。

図2の場合、Yが出店場所を変えるとYは得をするので、ナッシュ均衡ではありません。

図3はどうでしょうか。ビーチの真ん中に出店したXに対してYが少しだけビーチの左寄りに出店した場合です。Xの集客力は出店場所から右側のビーチ、対してYの集客力は出店場所から左側のビーチとなります。Yの集客力がXに劣っている状況です。

これではいけないとYがXの右側に出店すると、Yの集客力は増加します。したがって図3の場合もナッシュ均衡ではありません。結果このゲームは図1の出店場所になるのです。

このホテリングの法則は私たちの生活のあらゆるところに見られます。例えばコンビニチェーン。コンビニは品揃えも似通っているため、立地での差別化が必要です。そのため大通りに立つとコンビニチェーンが3店も4店も林立する、という状況が発生します。

牛丼チェーンやビジネスホテルが近接した場所に並ぶのも同じ原理です。

またホテリングの法則が有効なのは「地理的立地」だけに限りません。例えばスマートフォンの新製品がどれもよく似たルックス・機能であったり、コンパクトデジタルカメラがどれを買っても大差がないのも、ホテリングの法則で説明することができます。

競合業者が万人受けする無難な製品ばかりを発表する現象にはこんな構造があったのです。

・ホテリングの法則→「同じ商圏で全く同じ品質の同じ価格の製品を販売する2つの商店は、最終的に近接した場所に出店する」

・ホテリングの法則は「地理的立地」問題のナッシュ均衡を示している

・ホテリングの法則は「地理的立地」問題以外の状況にも当てはまる

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど