戦略形ゲームのモデルを理解する
ゲーム理論における「ゲーム」の最も基本的な形を「戦略形ゲーム」と呼びます。
このゲームを構成するのは「プレイヤー」「戦略」「利得」の3つの要素です。
これら3つの要素を表にしたものが「利得表」。戦力形ゲームとは、この利得表の形で表現されるゲームを指します。
戦略形ゲームは「同時手番ゲーム」とも呼ばれます。「同時手番」とは「同時に行動(=戦略)を選ぶ」という意味ですが、全く同じタイミングでなくとも、相手の戦略を把握していない状況で自分の戦略を選ぶのであれば、「同時手番ゲーム」です。
一般的なジャンケンは同じタイミングで戦略(グー・チョキ・パー)を選ぶゲームなので同時手番ゲームですが、例えば1人目がどの戦略を選ぶかをあらかじめ紙に書いて伏せておき、2人目の戦略を見てから勝敗を決めても、「同時手番ゲーム」と呼びます。
以下で代表的な戦略形ゲームの例を見て、このタイプのゲームについて理解を深めておきましょう。
例題-「囚人のジレンマ」
全く同じ軍事力を持つ、隣り合う2国、X国とY国があります。両国はできるならば戦争はしたくありませんが、もちろん隣国に攻め入られることも望みません。ある時X国の為政者が「軍事力を増強しよう!」と言い始めます。
このニュースを聞いたY国の為政者は「このままではいられない!我が国も軍事力を増強しよう!」と言い始めます。本来は戦争をしたくなかった両国は、この出来事以降競うように軍備拡大を進めていきます。
解説
このゲームのプレイヤーは「X国」「Y国」です。戦略はそれぞれ「軍備拡大」「軍備縮小」。利得は「政治的・軍事的な影響力」です。これを利得表にしたものが下図。
軍備拡大を進めるX国に対して、Y国が「戦争反対」を掲げ続けて軍備縮小に踏み切った場合、X国の利得は大きくなり(影響力増)、Y国の利得は小さくなります(影響力減)。
逆もまた然り。利得表の利得を示す欄の左側が表の左側のプレイヤー(この場合X国)の利得を示し、右側が表の上側のプレイヤー(この場合Y国)の利得を示します。
例えば利得表の利得が「2.-1」という表記であれば表の左側のプレーヤーは「2」の利得を得ていて、表の上側のプレーヤーは「-1」の利得を得ているということになります。
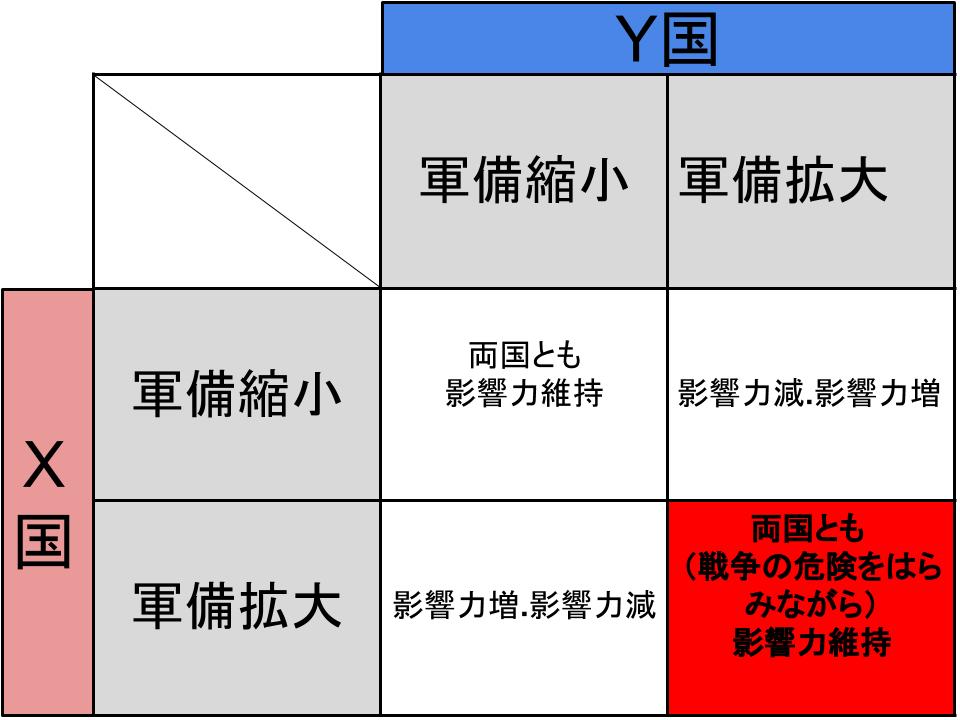
本来はどちらも戦争をしたくないので、両国とも軍備縮小を選択するのがベストです。しかし戦略的に、軍備縮小を選択すれば利得を奪われるリスクが大きくなります。結果、両国の選択肢は「軍備拡大」となるのです。
相手の戦略を推測し、自らの戦略を選ぶ。これが戦略形ゲームのモデルです。
例題-「居酒屋ゲーム」
同期入社のFさんとGさん。その日は花の金曜日、2人とも「ちょっとF(G)と飲みたいな」という気分になっています。かと言って「誰とでもいいから飲みたい」というわけでもありません。もしFさん(Gさん)が一緒に飲めないのであれば、自分もまっすぐ家に帰ろうと考えています。
解説
一見戦略など関係ないようなこのケースも、戦略形ゲームのモデルとして考えることができます。プレイヤーは「Fさん」「Gさん」。戦略は「居酒屋に行く」「まっすぐ帰る」です。利得は「楽しい気持ち」としましょう。
お互いに二人で居酒屋に行けば楽しいが、一人で行くくらいだったらまっすぐ家に帰った方がましだと考えています。
そこで、二人で居酒屋に行く場合の「楽しい気持ち」を2、一人で居酒屋に行く場合の「楽しい気持ち」は0、まっすぐ家に帰る場合の「楽しい気持ち」を1とすると、下図のような利得表が作られます。利得表が作られるということはすなわち「戦略形ゲームのモデル」です。
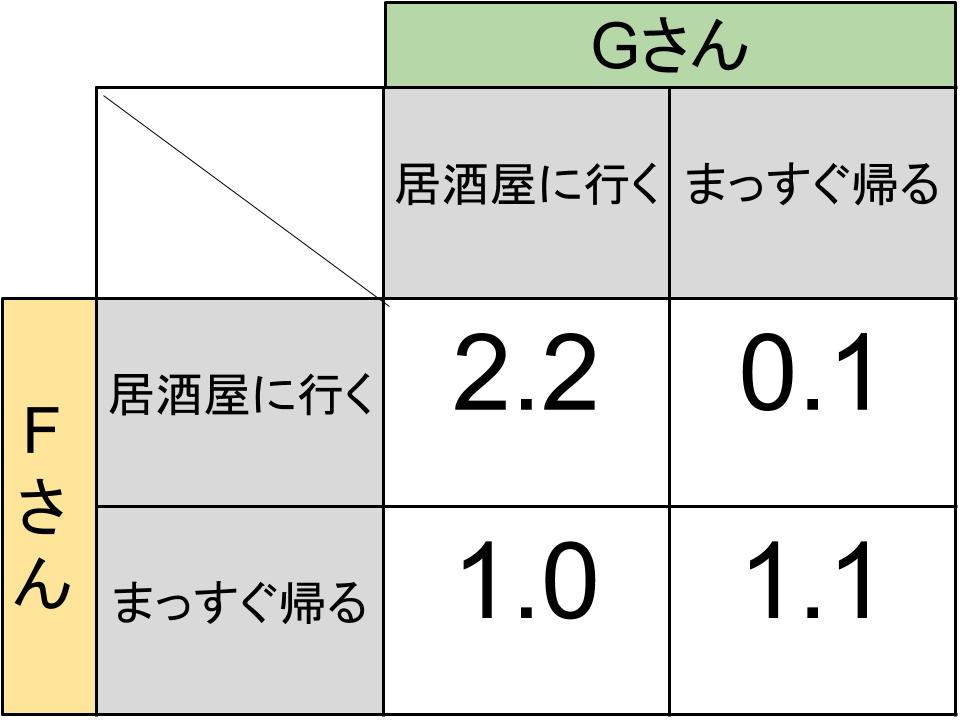
この利得表に従うとFさんとGさんは「今日飲みに行く?」と本人に聞かない限り、お互いに「あいつが行くなら飲みに行く」と相手の判断に自分の判断を依存させ合っているため、いつまでも解にたどり着けません。
これを「支配戦略のないゲーム」と言い、このモデルを「居酒屋ゲーム」と呼びます。
支配戦略(合理的な豚)
ゲーム的状況における戦略には、相手の戦略にかかわらず、自分にとってベストな戦略があります。これを「支配戦略」と呼びます。支配戦略を見つけることができれば、それ以外の戦略については考慮しなくていいので、意思決定が大幅に楽になるでしょう。
例題1
高校生のX君とYさんはグループ課題でペアを組むことになりました。真面目なYさんは課題をこなすためにX君に「どんなテーマにする?」と相談しに行きましたが、不真面目なX君は「そんなことより一緒に遊びに行かない?」とごまかしてばかり。協力しようとしてくれません。
自分が一生懸命やっても2人の評価になることを考えると、さすがの真面目なYさんも課題へのやる気がなくなってきました。「もういっそのこと私もサボっちゃおうか」。Yさんの心も揺らぎます。しかし課題を提出しないグループは、罰として校庭の掃除をさせられることになっています。
X君もYさんも校庭の掃除はしたくありません。この時のYさんの支配戦略は「課題をこなす」「サボる」どちらでしょうか。
解説
答えは「課題をこなす」です。X君が課題をサボろうが、気が変わって協力しようが、Yさんは課題に取り組むべきです。
X君がサボってもYさんが課題に取り組んでいれば校庭の掃除は免れます。もちろんX君が協力してくれれば課題はよりスムーズにこなせるでしょう。逆にYさんがサボってしまえば、「校庭の掃除」という最悪の事態が待っています。
したがって、Yさんの支配戦略は「課題をこなす」です。
1.jpg)
これと類似したゲームに「合理的な豚」があります。支配戦略を考えるにあたって代表的なモデルなので、ここで紹介しておきましょう。
例題-「合理的な豚」
体力が強く、かつ餌を食べるスピードも速い豚Fと、体力が弱く、かつ餌を食べるスピードが遅い豚Gがいます。
目の前には10単位分の餌が入っている餌箱があります。この箱の蓋をあけるためには箱から離れた場所にあるスイッチを押さなくてはなりません。これを押すためには餌2単位分の労力が必要です。
2匹の豚に用意された戦略は「スイッチを押しに行く」か「その場で待つ」かのいずれか。
2.jpg)
豚が2匹ともスイッチを押しに行くと、体力のある豚Fが先に餌箱に戻ってしまい、豚Gは餌を全く食べられません。この場合の利得はケース1。豚Fは労力2を使って餌10を食べられるので利得は8ですが、豚Gは労力2を払っても餌を食べられないのでマイナス2です。
では豚Fが「その場で待つ」を選び、豚Gが「スイッチを押しに行く」を選んだ場合はどうでしょうか。この場合の利得はケース2です。豚Gはただスイッチを押しただけで一切餌は食べられず、逆に豚Fは何もせずに餌を食べつくせるので10となります。
逆に豚Gが「その場で待つ」を選び、豚Fが「スイッチを押しに行く」を選んだとしましょう。豚Gは食べるのが遅いので、箱が開いた瞬間から食べ始めても豚Fが戻るまでに6単位分の餌を食べることしかできません。
豚Fが戻って来れば残りは全部豚Fが食べてしまうので、利得はケース3のようになります。労力を使わず餌を食べただけの豚Gは6、労力2を使って残った餌を食べた豚Fは2です。
2匹とも「その場で待つ」を選べば、どちらの豚も餌は食べられないので利得はそれぞれ0です。
解説
この場合の2匹の豚にとっての支配戦略を考えてみましょう。体力が弱く、かつ餌を食べるスピードも遅い豚Gにとっての支配戦略は「その場で待つ」です。
豚Gにとってはスイッチを押しに行っても単に労力を消費するだけだからです(ケース1とケース2)。であればいっそ食べられなくてもその場で待っているほうが利得は大きくなります(ケース4)。
豚Fがスイッチを押しに行けば、自分は6単位分の餌が食べられるので最も利得が大きくなります(ケース3)。したがって豚Gはどんな場合でも「その場で待つ」べきなのです。
対して体力が強く、かつ餌を食べるスピードも速い豚Fには支配戦略がありません。豚Gが「その場で待つ」を選ぶのであれば自分がスイッチを入れに行かなければ餌を食べることができませんし、豚Gが「スイッチを押しに行く」を選べば自分はその場で待っているのが正解となります。
相手の戦略によって自分の選ぶべき戦略が変わるので、「相手の戦略にかかわらず、自分にとってベストな戦略」はないのです。
ここで豚Fがするべきは、豚Gの出方を予測することです。この2匹の豚は「合理的な豚」なので、自分の利得が最大化する戦略を選ぶことができます。
したがって豚Gは「その場で待つ」を選択するでしょう。豚Fはこの豚Gの戦略を予測することができるので、豚Fは自分の利得を最大化するために「スイッチを押しに行く」を選ばざるを得ません。
「合理的な豚」というゲームは、体力も強く、餌を食べるスピードも速いにもかかわらず、豚Fは豚Gにより多くの餌を食べられながら、自分はスイッチを押しに行くしかできないという皮肉な結果となります。
支配される戦略の繰り返し消去
ゲーム的状況において、自分以外のプレイヤーがどんな戦略を選んでも自分にとって利得が最も大きくなる戦略を「支配戦略」と呼びます。
この支配戦略として選ばれなかった戦略を「支配される戦略」と呼びます。支配される戦略はゲーム的状況の解を導き出すための重要なヒントです。
以下の例題では支配される戦略を見つけることで、解を導き出す方法を紹介します。
例題2
表1のような利得表を構成するゲーム的状況があります。この場合の解を「支配される戦略」を基に考えてみましょう。
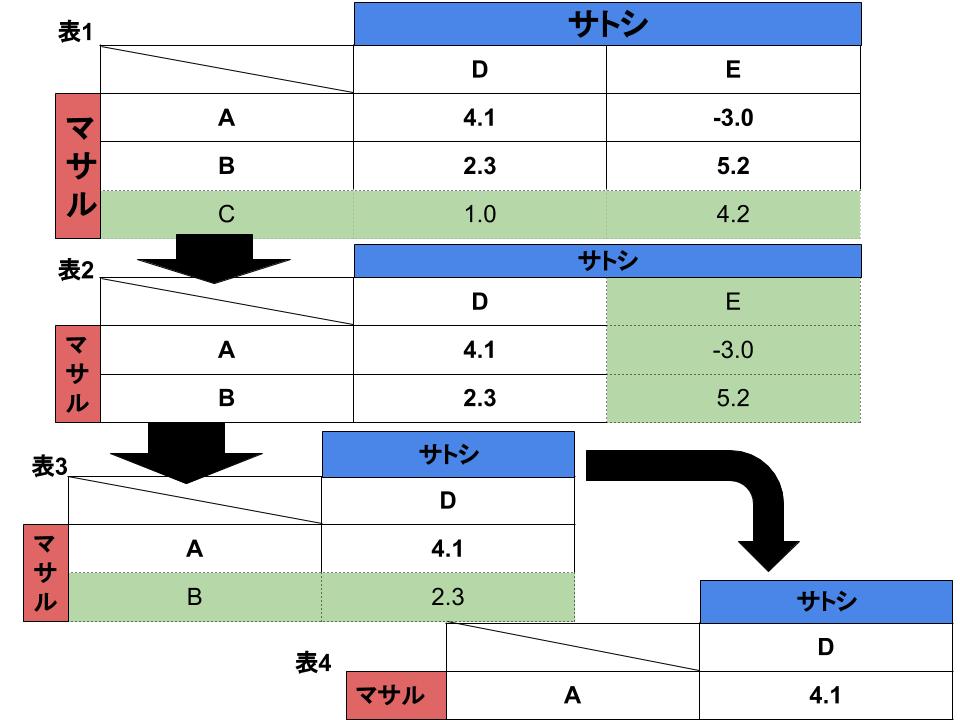
解説
マサルにとっての戦略はA〜Cです。この3つのうち、BとCはサトシがどの戦略を選んでもBのほうがマサルにとって利得の大きな戦略になります。すなわち「CはBに支配される」戦略です。したがってマサルがCを選択することはないので、Cは消去されます(表2)。
次にサトシの戦略について考えてみましょう。マサルがAかB、どちらの戦略を選択しても、サトシにとってはDのほうが利得が大きくなります。このとき「EはDに支配される」と言います。したがってサトシがEを選択することはないので、Eは消去されます(表3)。
では残るAとBのうち、どちらが支配される戦略でしょうか。サトシはすでにDしか選ばないことがわかっているので、マサルはより利得の大きいAを選ぶのが合理的な判断です。つまり「BはAに支配される」戦略となります。
したがって表4のようにBは消去され、マサルはAをサトシはDを選ぶのがこのゲーム的状況の解となります。
消去法で意思決定する
「支配される戦略」を基に、戦略を消去していく方法を「支配される戦略の繰り返し消去」と言います。一見専門用語のように見えますが、これは私たちが日常的に行っている「消去法」とよく似た考え方です。
次のようなゲーム的状況は私たちが日常でも出くわす状況ですが、無意識のうちに「支配される戦略の繰り返し消去」を行っていることがわかります。
例題3
Sさんは近所のコンビニYにいつものように出かけました。Yは大手コンビニチェーンなので基本的に値引きは行わず、いつも定価で販売しています。
しかしその日Sさんが来店すると、いつもSさんが買う定価300円の缶ビールの中に1本だけ280円の値札が貼られた商品があります。中身も容量も全く同じビールなのに、お店側のミスなのか、それだけ20円安く販売されているのです。
「これはラッキーだ!」とSさんは280円の缶ビールを手に取り、レジへと持って行きました。
コンビニYとしてはすでにその価格で陳列されていた商品なので売らないわけにはいきません。値札が間違っていることに気づきながらも、店員は渋々280円で缶ビールを販売しました。
解説
一見日常でも起こりそうなワンシーンですが、この状況を利得表にすると下図のようになります。
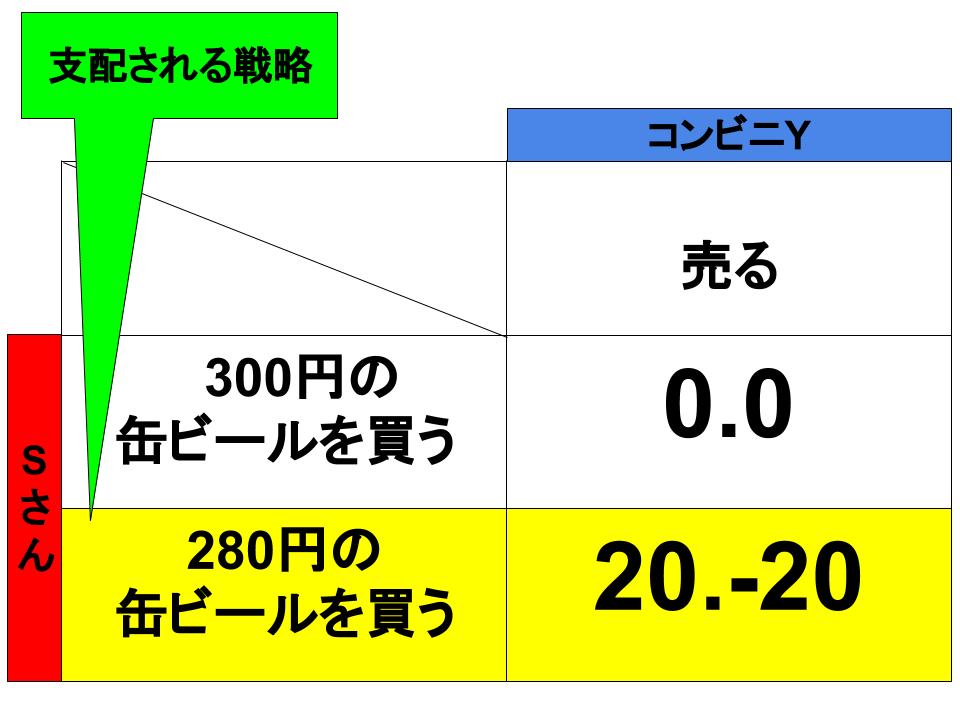
プレイヤーは「Sさん」と「コンビニY」です。Sさんはいつも缶ビールを購入するので「買わない」という戦略はなく、「300円の缶ビールを買う」か「280円の缶ビールを買う」かどちらかの戦略しかありません。
対してコンビニYが「売らない」という戦略を選べないとすると、「売る」という戦略しかありません。
この状況において「300円の缶ビールを買う」は「280円の缶ビールを買う」に支配される戦略です。したがって「300円の缶ビールを買う」という戦略は消去され、このゲーム的状況の解は黄色の枠のケースになります。
このように私たちは日常的に「支配される戦略の繰り返し消去」を行っているのです。選ぶことのできる戦略が増えたり、利得の数字が複雑化しても、このコンビニの例を使えば難しく考えることなく「支配される戦略の繰り返し消去」を行うことができるでしょう。
支配戦略のないゲーム
ゲーム的状況において相手の戦略に関わらず、自分の利得が最も大きくなる戦略が「支配戦略」です。支配戦略は意思決定をする上で重要なヒントになりますが、状況によっては支配戦略のないゲームも存在します。
支配戦略のないゲームでは自分の戦略も、相手の戦略も、お互いの選択に応じて変化するため、相手の戦略を予想することができません。したがって解にたどり着くこともできなくなります。
はじめに「戦略型ゲームのモデル」でも紹介した「居酒屋ゲーム」と呼ばれる例を見ておきましょう。
例題4
同期のXとYはお互いに仕事を終え、帰りのエレベーターで一緒になります。「久しぶりだなあ」。2人は1年目までは同じ部署でしたが、2年目から別の部署で働いてきたのです。
ふとXは「もし今日こいつが居酒屋に飲みに行くっていうなら一緒に飲みたいなあ(自分から誘うほどではないけど)」と思いました。偶然、Yも同じことを考えています。
それと同時に「もしこいつが行かないっていうなら、1人で飲みに行きたいわけじゃないし、まっすぐ帰ろう(あくまで自分から誘うほどではないけど)」とも考えていました。
エレベーターの階数表示は刻々とエントランスのある1階に近づいています。さてこのゲーム的状況の解はどこにあるでしょうか。
解説
答えは「解にはたどり着けない」です。この2人は互いに相手の戦略に自分の意思決定を依存させているので、下図のように戦略の予測が堂々巡りになってしまいます。もしどちらかが「この後飲みに行かないか?」と誘わない限り、2人の乗ったエレベーターはこのままエントランスのある1階に到着してしまうでしょう。
これが居酒屋ゲームです。居酒屋ゲームは勝負事ではありませんが、これと同じ状況は勝負事でも起こりえます。次にその例を見ておきましょう。
例題5
F店とG店は互いにアパレルショップを経営しています。F店の店長が今年流行ると考えているカーディガンの色は「グレー」と「ネイビー」。G店の店長が今年流行ると考えているのは「ベージュ」と「カーキ」です。
両店は競合なので、それぞれが打ち出すカラーによって売り上げ(利得)が変動します。利得表が次のようになる場合、両店はどのような意思決定をするでしょうか。
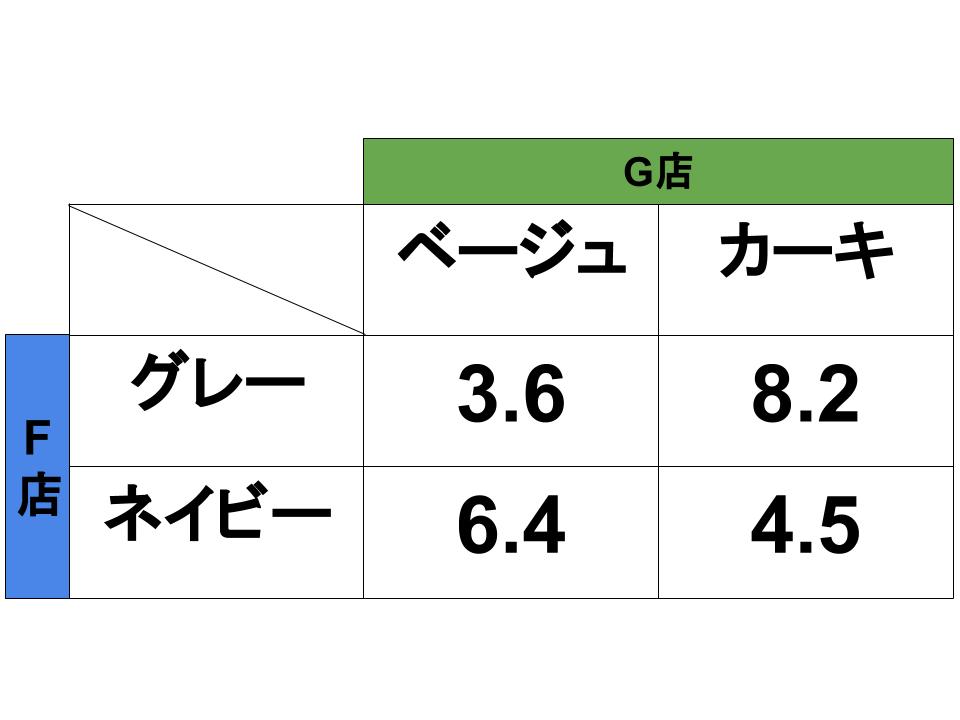
解説
F店とG店は互いの戦略を予想しながら、自店が最も大きな利得を得ようとします。F店にとってみればG店が「ベージュ」をプッシュした場合、「ネイビー」をプッシュしたほうが利得は大きくなりますが、G店が「カーキ」をプッシュした場合にF店が選ぶべき戦略は「グレー」です。
これはG店にとっても同じで、F店がプッシュするカラーによって自店の戦略も左右されてしまいます。この状況は「居酒屋ゲーム」と全く同じ状況です。相手の戦略を予想しようとするほど堂々巡りとなり、いつまでもF店とG店は自店の方針を決められないままになります。
混合戦略と純粋戦略
このような状況を打破するためにゲーム理論が提案するのが「混合戦略」と呼ばれるものです。混合戦略とは、相手に戦略を読まれないように確率的に戦略を混ぜる方法を言います。
例えばF店が3分の1の確率で「グレー」をプッシュし、3分の2の確率で「ネイビー」をプッシュする戦略をとった場合などが混合戦略です。
これに対して、確率的に戦略を選ぶのではなく、グレーならグレー、ネイビーならネイビーという選び方を「純粋戦略」と呼びます。
まとめ
・戦略形ゲームの定義→利得表の形で表現されるゲーム
・戦略形ゲームの構成要素→「プレイヤー」「戦略」「利得」
・戦略形ゲーム=同時手番ゲーム
・支配戦略=「相手の戦略にかかわらず、自分にとってベストな戦略」
・支配戦略として選ばれなかった戦略を「支配される戦略」と呼ぶ
・「支配される戦略」を基に、戦略を消去していく方法を「支配される戦略の繰り返し消去」と呼ぶ
・「支配される戦略の繰り返し消去」は私たちが日常的に行っている「消去法」と同じ
・支配戦略のないゲームでは相手の戦略に自分の戦略が依存するため、解にたどり着けなくなる
・確率的に戦略を混ぜる方法を「混合戦略」と呼ぶ
・確率的な戦略の選択をしない方法を「純粋戦略」と呼ぶ
関連ページ
- ゲーム理論とは…意味を理解してビジネスの駆け引きの現場で活かす
- 交互進行ゲーム(逐次手番ゲーム)とゲームの木
- ゲーム理論の視点からオークションの仕組みを理解する
- ベイズ均衡(ベイジアンナッシュ均衡)
- 男女の争いとチキンゲーム
- コーディネーションゲーム(失敗と解決法)
- クールノー競争とベルトラン競争
- ゲーム理論の基本を理解する(囚人のジレンマ)
- ホテリングの立地ゲーム
- 情報非対称ゲーム(不完備情報のゲーム)
- ミニマックス定理
- 混合戦略と純粋戦略
- ナッシュ均衡を理解する
- 部分ゲーム完全均衡と後ろ向き帰納法
- 囚人のジレンマの解決法
- 戦略形ゲームのモデルを理解する
- 脅しのゲームと信頼のゲーム
- 交互進行ゲームにおける戦略と信頼性のない脅し
