ゲーム理論とは…意味を理解してビジネスの駆け引きの現場で活かす

トップページ＞ゲーム理論＞ゲーム理論とは…意味を理解してビジネスの駆け引きの現場で活かす

ゲーム理論とは…意味を理解してビジネスの駆け引きの現場で活かす

20世紀前半に数学者フォイ・ノイマンと経済学者モルゲンシュテルンによって創られた理論「ゲーム理論」。

学問の分野としては経済学に分類されるこの理論は、今なお様々な発展を見せています。しかし「ゲーム」という楽しげなネーミングとは裏腹に、かなり難解な部分も多く、実際に習得するのは難しい理論でもありるのです。

こではまず、ゲーム理論がどのような目的で考案され、現代社会にいかに適用されるかについて考えていきます。

駆け引きを科学せよ！ゲーム理論概要

はじめにゲーム理論が何を学問する理論なのかについて知っておきましょう。それは、「駆け引き」です。

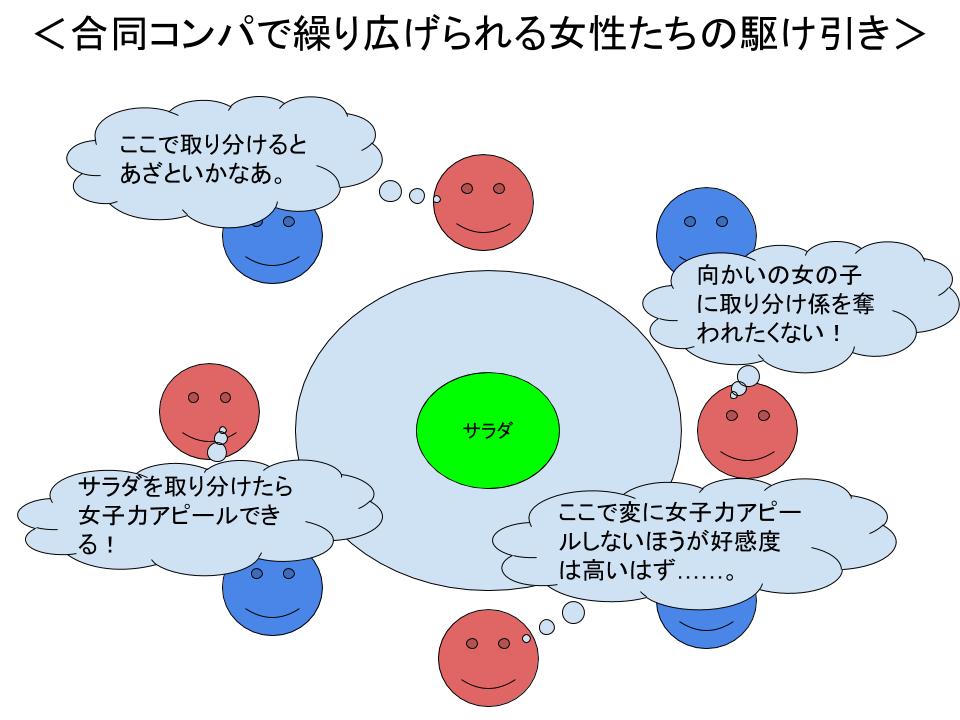
企業内であなたのチームのプロジェクトを採用に導くために、チーム内で意思決定を行う場合はもちろん、異性との合同コンパで運ばれてきたサラダを誰が取り分けるのかなど、私たちの日常には数多くの駆け引きがあります。

自分の発言によって別の人間がどのように動くのか、その人間の行動によって自分はどのように動くことができるのか。これらを考えるのがゲーム理論なのです。

そのため、ゲーム理論を身につければ、ビジネスシーンはもちろん、人間関係においても科学的に自分の行動を決定することができます。

ゲーム理論（合コンの駆け引き）

市場メカニズムとゲーム理論

ゲーム理論はビジネスや日常生活にも役立つと言いましたが、この理論がそのために考案されたというわけではありません。市場メカニズムすなわち「市場における需要と供給の理論」は、ゲーム理論が考案された時にもすでに強力な説得力を持っていました。

しかし、全ての経済現象がこの市場メカニズムだけで説明できるわけではなかったのです。

ノイマン氏とモルゲンシュテルン氏は、この市場メカニズムの「穴」を埋めるために、人間が意思決定を行う際の「駆け引き」を分析するためのツールが必要だと考えます。そうして発表されたのが『ゲームの理論と経済行動』（1944）という本でした。

発表から70年以上経った今、ゲーム理論は経済学の重要な一分野に成長し、複雑化が進む経済を説明するための重要なツールとなっています。

例題

以下のような状況を思い浮かべて、その時に生じる「駆け引き」について考えてみましょう。

・お手伝いはしたくないがお小遣いが欲しい子供と、子供の成長を考える親。この両者の間の駆け引きはどのようなものか？

・中華料理が食べたい自分と、イタリアンが食べたい恋人。中華料理店に連れて行くためにはどのような駆け引きが必要？

・コストカットを考えるA社と、利益アップを考える取引先のB社。両社が商談をする時、どのような駆け引きがされる？

・軍事力が高いが資源のないA国と、資源はあるが軍事力がないB国。両国がC国の領土を奪い合うとどのような駆け引きがされるか？

・給料を上げて欲しい労働組合と、給料を上げたくない経営側。両者にはどのような駆け引きが起きる？

解説

こういった状況をゲーム理論では「ゲーム的状況」と呼び、そこに参加する人間（イタリアンが食べたい恋人など）を「プレイヤー」と呼びます。

5つの例からもわかるように、私たちは日々ゲーム的状況にさらされているのです。これらを分析するゲーム理論を身につければ、日常のゲーム的状況を有利に進めることができるでしょう。

駆け引きの本質を見抜くゲーム理論

駆け引きを科学的に考えても、その全てを説明できるわけではありません。しかし、ゲーム理論の持つ視点を使えば、駆け引きの場面でよく使われる「直感」「長年の勘」といったものの正体を分析し、科学的な説明を加えることができます。

それができれば、10年や20年のキャリアがなくとも、重要な場面で最善の判断を下す人材を育成できる可能性が出てくるでしょう。あるいは恋人との喧嘩にゲーム理論を当てはめて、状況を客観的に分析することも可能かもしれません。

ゲーム理論を身につければ、駆け引きの全てではなくとも、本質を見抜くことができるようになるのです。

ゲーム理論の歴史

ゲーム理論は1944年に考案されて以降70年の歳月を経てなお発展し続ける経済学の学問分野です。しかし、この理論も初めから現在のように経済学の中で存在感を持っていたわけではありません。

ここではゲーム理論が生まれた黎明期から現在に至るまでの、ゲーム理論の歴史について紹介します。

ゲーム理論の黎明期

1944年、数学者フォン・ノイマン氏と経済学者のモルゲンシュテルン氏が出版した『ゲームの理論と経済的行動』をきっかけにゲーム理論は誕生しました。

市場メカニズムが説明できない細かな人間の意思決定を説明するために考案された理論でしたが、手法はとても難解で、かつ数学的でした。つまり、実際の経済現象にそのまま当てはめられるようなものではなかったのです。

しかし、経済現象を複数の人物（プレイヤー）がルールに従ってゲームを展開する場として見立てた点においては、彼らの着目点は鋭かったと言えます。

複雑に絡み合う「自分の意思決定」と「他者の意思決定」。どのように考えれば「他者の意思決定」を予測することができるのか。これらを体系的に分析しようとしたパイオニアが、ノイマン氏とモルゲンシュテルン氏だったのです。

ゲーム理論を大幅に発展させた「ナッシュ均衡」

2人が考案したゲーム理論を大幅に発展させたのが、映画『ビューティフル・ライフ』でも有名になった数学者ナッシュ氏です。彼がこの理論に導入したのが「ナッシュ均衡」として知られる概念でした。

ナッシュ均衡は「みんなが幸せになる選択肢」と言い換えられます。

例として、ラーメン店を経営するA店とB店があったとしましょう。

両店は新メニューにとんこつラーメンと味噌ラーメンどちらを追加しようかと悩んでいます。両店ともとんこつラーメンをメニューに追加すれば、A店の利益は40％増、B店の利益は20％増。両店とも味噌ラーメンを追加すると、両店とも25％の利益増が見込めます。

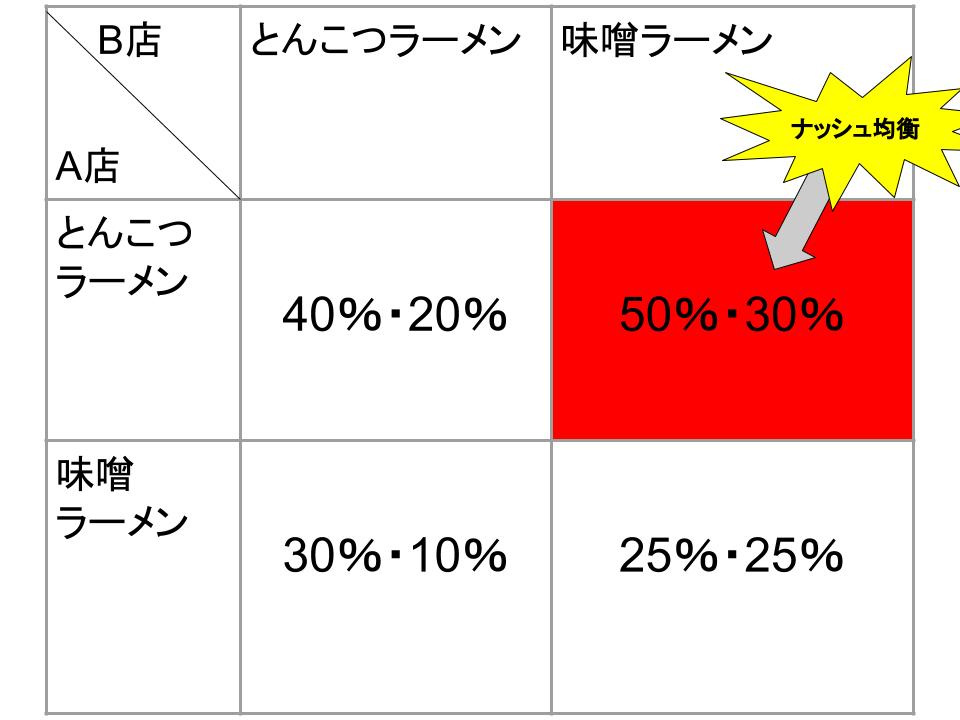
ゲーム理論（ナッシュ均衡）

両店の意思決定には上図の通り4パターンがありますが、そのうち両店の利益増がどちらにとっても最大になるのが赤く塗りつぶされた「A店はとんこつラーメン、B店は味噌ラーメン」の部分です。この選択肢を「ナッシュ均衡」と呼びます。

これによってゲーム理論は大幅に実社会に近づいた理論となりました。しかし経済学がゲーム理論を積極的に取り入れるという段階には、まだまだ時間が必要だったのです。

ゲーム理論、実社会に適用される

ゲーム理論がさらに実社会に近づくのは、1960年以降にハルサニ氏とゼルテン氏によって「情報不完備ゲーム」「部分ゲーム完全均衡」などが導入される頃です。

情報不完備ゲームとは、ゲームに参加するプレイヤーが同じルールを共有できていないゲームを指します。

例えば、A社とB社が市場を奪い合う場合に明確なルールはなく、むしろイノベーションは既存の価値観を壊すことによって生まれるものです。一般的な経済はこの情報不完備ゲームであり、スポーツのようにプレイヤー同士でルールが共有されている情報完備ゲームではありません。

「部分ゲーム完全均衡」はこのような情報不完備ゲームの中で、それぞれのプレイヤーが自分の持っている情報に基づいた自身にとっての最善の行動を指します。

これも実際の経済により近いゲームを想定することができるものです。

1970年以降になると、これらを用いて情報やインセンティブ、契約や企業組織などの実社会に即したテーマに、積極的にゲーム理論を活用するという流れができていきます。

いまやゲーム理論は経済学に必要不可欠

現在のゲーム理論は、ミクロ経済のみならずマクロ経済や組織、貿易、金融など、あらゆる分野に活用されるようになっています。

ゲーム理論を含む現代の経済学には複雑な計算が必要ですが、コンピューターの演算能力の向上も、この発展に大いに役立っていると言えるでしょう。今後、ゲーム理論は経済学の中でさらに大きな存在感を持つようになるはずです。

ゲーム理論の分類

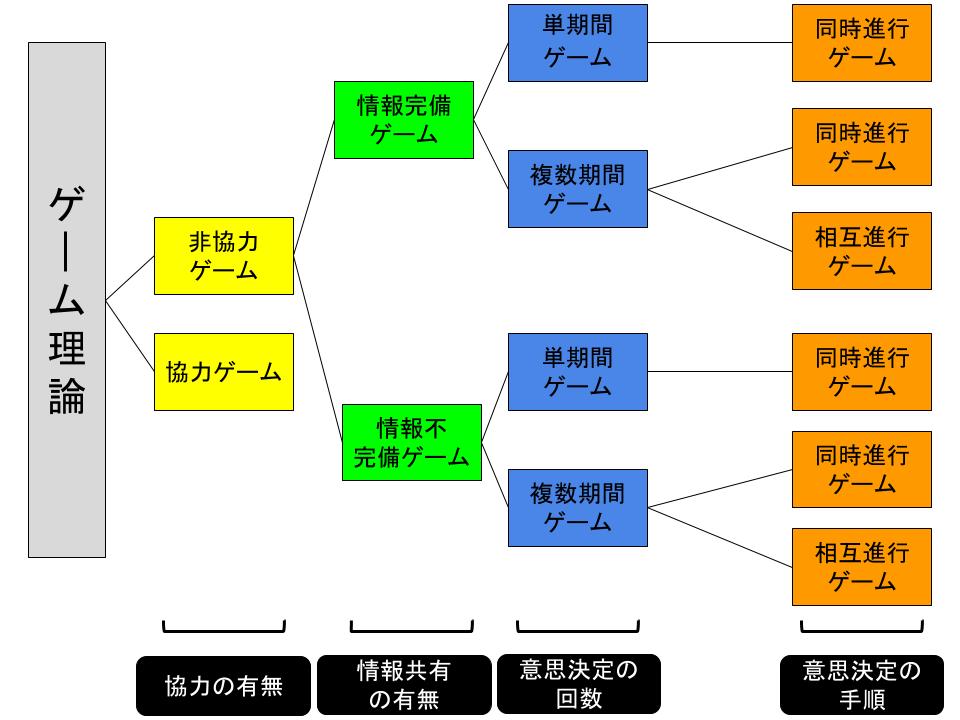
ゲーム理論で取り扱うゲーム的状況（駆け引き）は、スポーツのようなルールの決まった状況とは限りません。ゲーム的状況は、「プレイヤー同士の協力の有無」「情報の共有の有無」「意思決定の回数の多少」「意思決定の手順の違い」という4つの段階で分類されます。

ここからは、これらの分類とそれぞれの状況の大まかな説明をしていきます。

協力の有無による分類

最初のゲーム的状況の分類は「協力の有無」によって行なわれます。

協力というのはゲームに参加するプレイヤー同士の協力のこと。非協力ゲームではプレイヤー個人が自身の意志のみによって判断を下します。対して協力ゲームでは、プレイヤー同士が戦略を決定するために話し合い、合意を形成することが可能です。

非協力ゲームの典型は「2人ゼロサムゲーム」です。ゼロサムゲームとは「勝つか負けるか」が必ず決まるゲームを指します。2人でこのゲームをする場合、協力関係は有り得ません。

対して3つの企業が業務提携をする場合の意思決定は協力ゲームの典型と言えます。

情報共有の有無による分類

次の分類は「情報共有の有無」によって行なわれます。

プレイヤー同士で情報が完全に共有されている場合が「情報完備ゲーム」、そうでない場合が「情報不完備ゲーム」です。

じゃんけんは典型的な情報完備ゲームで、お互いが「グー」「チョキ」「パー」の三手しか出せないことを知っており、どの組み合わせで勝ち負けが決まるのかがはっきりしています。他にも将棋やチェスなども情報完備の典型です。

対して情報不完備ゲームは、プレイヤーの間に情報量の差がある状況を指します。AさんとBさんがデザートを取り合っていて、Aさんは冷蔵庫にプリンしかないと思っているのに対し、Bさんは冷蔵庫にプリンとティラミスがあることを知っている場合、この状況は情報不完備ゲームです。

ゲームをさらに複雑にする分類

情報完備ゲームと情報不完備ゲームはさらに「意思決定の回数」によって分類されます。

意思決定が1回だけのゲームが「単期間ゲーム」、複数回繰り返されるものが「複数期間ゲーム」です。

これをさらに「意思決定の手順」で分類したものが「同時進行ゲーム」と「交互進行ゲーム」となります。前者は複数のプレイヤーが同時に意思決定を行うゲームで、後者は交互に意思決定を行うゲームです。

1回のじゃんけんで2人のプレイヤーが勝敗を決定するゲームは「情報完備」かつ「単期間」かつ「同時進行」のゲームです。対してトランプの「大富豪」は「情報完備」かつ「複数期間」かつ「相互進行」のゲームと言えます。

このように分類されるにつれて、ゲームはより複雑になっていくのです。

ゲーム理論の分類

ゲーム的状況を分類する理由

これらの分類をすることでゲーム理論はプレイヤー間の情報構造や意思決定、利害関係、協力関係を数学的に分析できるようになっています。

ゲーム的状況の分類を理解しておけば、目の前で起きているゲーム的状況の本質が瞬時に見分けられるはずです。あなたが置かれているゲーム的状況がわかれば、自ずとどのような意思決定の仕方をすればいいかも見えてきます。

まとめ

・ゲーム理論とは「駆け引き」を科学する学問である

・ゲーム理論は元来、市場メカニズムの欠点を埋めるために考案された

・私たちはプレイヤーとして常にゲーム的状況にさらされている

・ゲーム理論で駆け引きの全てを理解できないが、駆け引きの本質は見抜くことができる

・ノイマン氏とモルゲンシュテルン氏がゲーム理論を考案した頃は、まだ実用的な理論とは言えなかった

・「ナッシュ均衡」の導入によって、ゲーム理論が実社会に適用される端緒が開かれた

・「情報不完備ゲーム」「部分ゲーム完全均衡」などの導入によって、ゲーム理論は徐々に実社会に適用されるようになっていった

・現代の経済学の中でゲーム理論はあらゆる分野に適用されている

・ゲーム理論の分類は「協力の有無」「情報共有の有無」「意思決定の回数」「意思決定の手順」によって行なわれる

・協力の有無による分類は「協力ゲーム」「非協力ゲーム」

・情報共有の有無による分類は「情報完備ゲーム」「情報不完備ゲーム」

・意思決定の回数による分類は「単期間ゲーム」「複数期間ゲーム」

・意思決定の手順による分類は「同時進行ゲーム」「相互進行ゲーム」

・分類が進むにつれて、ゲームは複雑化する

・ゲーム的状況の分類を理解していれば、自身が直面するゲーム的状況の性質が見抜ける

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど