リースファクター（年金現価係数）その2

トップページ＞ファイナンス（財務）＞リースファクター（年金現価係数）その2

【リースファクター（年金現価係数）とは】
ここまでで学んだように、リースファクター（年金現価係数）とは、「期間を現在価値に修正する」という考え方です。
（ここからはより一般的な年金現価係数という用語を使用します。）

上記では3年と5年という短い期間だったため、すべてを計算しましたが、これが20年、30年となると計算には時間と手間がかかり、計算ミスの可能性も大きくなっていきます。

よって年金現価係数を一度で導く方法を考えてみましょう。

実は年金現価係数は、現在価値と永続価値の考え方を使って以下のように考えることで、その計算式を導くことができます。

なお、ここでは計算したい期間をn、割引率をrとします。

分子は自動車のリースのときと同様1です。

1．現在にいると仮定し、1年目から∞年後までの現在価値を計算する
2．n年後になったと仮定し、n＋1年目から∞年後までの現在価値を計算する
3．1から2を引く

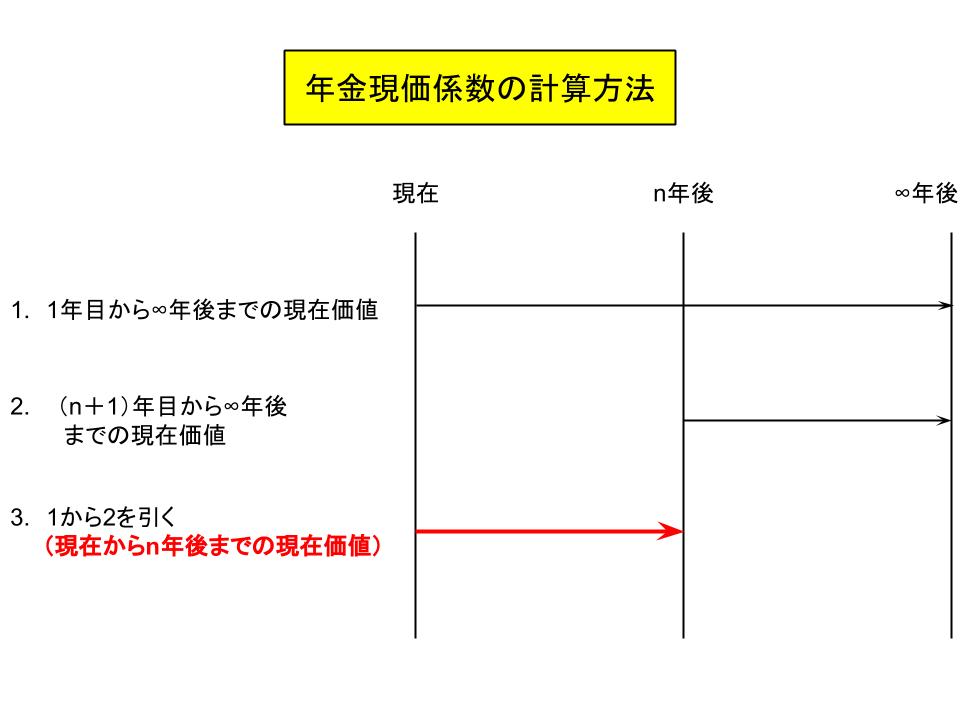
リースファクター（年金現価係数）

例えば30年の年金現価係数を知りたい場合は、

1．現在から見た永続価値を求め、
2．30年後から見た永続価値を求めてそれを現在価値に修正し、
3．1から2を引く、ということです。

少しややこしいですが、1年ごとに求めるのではなく、「現在の永続価値」と「30年後の永続価値と現在価値の差」から求めるということです。

では実際に計算してみましょう。

1．現在にいると仮定し、1年目から∞年後までの現在価値を計算する
まず1年目から∞年後までの現在価値は、以下のようになります。

PV　＝　1÷r

これはまさにCFを1と考えた場合の永続価値です。

2．n年後になったと仮定し、n＋1年目から∞年後までの現在価値を計算する
つぎにn年経過したと仮定し、n＋1年目から∞年後までの現在価値を計算します。

まず、n年から見たn＋1年目から∞年後までの現在価値は以下です。

n年目から見たPV　＝　1÷r

現在から見てもn年後から見ても、永続価値は同じになります。

どの時点から考えても、終わりが「∞年後」である以上は永続価値は同じということです。

そしてこれはn年後からの永続価値なので、現在価値に割り引きます。

PV　＝　（1÷r）÷（1＋r）n

これがn年後から見たn＋1年目から∞年後までの現在価値です。

3．1から2を引く
ここで、1から2を引くことで現在からn年後までの現在価値を算出することができます。

PV　＝　（1÷r）−（（1÷r）÷（1＋r）n）

これを計算していきます。

PV　＝　（1÷r）−（（1÷r）÷（1＋r）n）
　↓
PV　＝　（1÷r）−（1÷r（1＋r）n）
　↓
PV　＝　（（1＋r）n÷r（1＋r）n）−（1÷r（1＋r）n）

これをまとめると、最終的に現在価値は以下のようになります。

PV　＝　（（1＋r）n−1）÷r（1＋r）n

これが年金現価係数の計算式となります。

【年金現価係数と複利現価係数】
年金現価係数は期間の現在価値と考えることができるので、例えば一定期間CFが一定の場合、CFに年金現価係数をかけることで一気にその期間の現在価値を計算することができます。

例えば冒頭に出てきた自動車Aの年間費用について考えてみましょう。

自動車Aの年間費用（100）の現在価値は以下のように計算しました。

PV　＝　100÷（1.1）＋100÷（1.1）2＋100÷（1.1）3　≒　90.91＋82.64＋75.13　＝　248．68

ここで、「PV　＝　（（1＋r）n−1）÷r（1＋r）n」を使って、割引率を10％とする3年の年金現価係数を計算してみます。

PV　＝　（（1＋0.1）3−1）÷0.1（1＋0.1）3　＝　0.331÷0.1331　≒　2.4869

そして自動車Aの年間費用（100）にこの年金現価係数をかけると、年間費用の現在価値となります。

PV　＝　100×2.4869　＝248.69

これは、上記の個別に計算したPVと一致しています。
（末尾が異なりますが、これは計算過程で少数点以下を四捨五入している関係です。）

このように、年金現価係数は期間を割り引くという考え方ですので、一定のCFが発生する場合であれば、どんな場合でも使用できます。

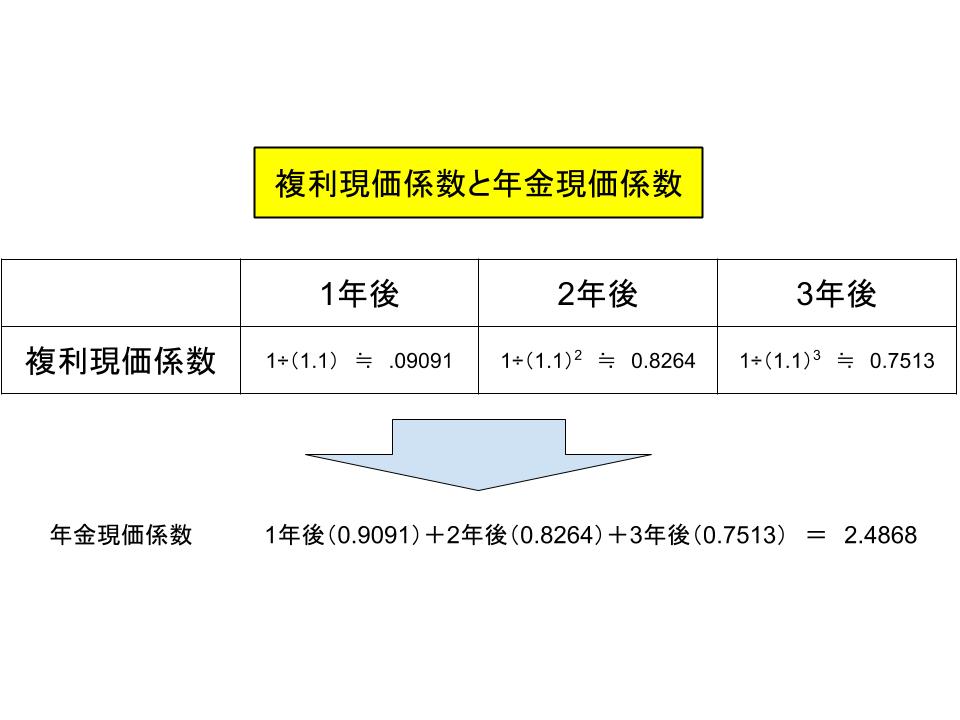
また、年金現価係数は、「複利現価係数」を加算したものです。

複利現価係数とは、リース費用計算の最初で1年ずつ個別に現在価値を計算していった際の個別の値です。

例えば1年後の現在価値である「1÷（1.1）　≒　.09091」、2年後の現在価値である「1÷（1.1）2　≒　0.8264」、3年後の現在価値である「1÷（1.1）3　≒　0.7513」は、すべて「複利現価係数」です。

複利現価係数をすべて加算したものが年金現価係数になるということです。

リースファクター（年金現価係数）

なお、年金現価係数については、上述したように預金の元本計算などでも使用されます。

それらについてはここでは触れませんが、永続価値と現在価値の考え方を使用した年金現価係数には様々な使い道があることを理解しておきましょう。

現在価値という考え方は非常に複雑ですが、キャッシュフロー同様ファイナンスを学ぶ際になくてはならない考え方の一つです。

そしてその計算をスムーズに行えるように必要なことは、何よりも「慣れ」です。

最初はとまどうことも多いですが、慣れるとさほど苦労なく計算ができるようになります。

何度も概念と考え方を見直し、実際に計算を繰り返すことで「慣れ」を身に着けていきましょう。

前のページ　「リースファクター（年金現価係数）その1」

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど