CAPMの公式と解明 その1
【CAPMの公式と解明】
自動車部品製造会社であるS社に勤めるMさんは、上司から個別資産のリスクとリターンを表すCAPM（資本資産評価モデル）という概念を教えてもらい、CAPMを計算するためにはβ（ベータ）という値の意味を理解することが重要だということを学びました。
そしてβを学んだMさんは個別資産のCAPMについて自分で考えてみようと思い、その公式を導いてみることにしました。
【CAPM（資本資産評価モデル）の公式の導出】
CAPMは個別の株式の期待収益率を定量化する理論です。
そして個別の株式の期待収益率は、その株式のリスクとリターンの度合いから決定されます。
その根拠となるのが、市場全体のポートフォリオとも言えるマーケットポートフォリオとβ（ベータ）です。
βはマーケットポートフォリオに対して、個別の株式がどの程度リスクがあるかを見る指標です。
よってMさんは、以下のように考えました。
個別の株式の期待収益率 ＝ β（ベータ）×マーケットポートフォリオの期待収益率
βはマーケットポートフォリオに対するリスクとリターンの大きさの度合いを表します。
よってマーケットポートフォリオにβをかけることで、個別の株式の期待収益率は出せるはずです。
しかし、そこにたまたま通りかかったNさんが、Mさんが考えた式を見て、以下のような指摘をしました。
≪Nさんの指摘≫
「君の考え方でいくと、βが0のときは必然的に個別の株式の期待収益率も0ということになるよね。ただ、その考え方だと、リスクフリー資産が存在しないことになってしまうよ。資本市場線を思い出すといいと思う。リスクフリーレートを持つ国債などのリスクフリー資産の存在がある限り、投資家はいくらリスクが0でもリターンが0の会社には投資はしないはずだよ。」
Mさんは資本市場線を思い出し、確かにその通りだと考えて今度は以下のような式を導きました。
個別の株式の期待収益率 ＝リスクフリーレート＋ β（ベータ）×マーケットポートフォリオの期待収益率
そしてMさんはこの式で正しいと仮定し、以下の条件の下で同業の上場企業K社の期待収益率を計算してみることとしました。
・リスクフリーレート 2％
・同業の上場企業のβ 1
・マーケットポートフォリオの期待収益率 6％
K社の株式の期待収益率 ＝ 2＋1×6 ＝ 8％
しかし、今度はMさんが自ら式の矛盾に気づくこととなりました。
本来βが1の場合は、期待収益率はマーケットポートフォリオと同じ1でなければならないはずなのです。
しかしここではリスクフリーレートの分、収益率が大きくなってしまっています。
そこでMさんはもう一度考えることにしました。
リスクフリーレートが存在しても、βが1の場合の個別の株式の期待収益率はマーケットポートフォリオと同じ1にならなければならないのです。
そこでMさんは図示して考えてみようと思い、横をβ、縦を期待収益率として、以下のように考えてみることにしました。
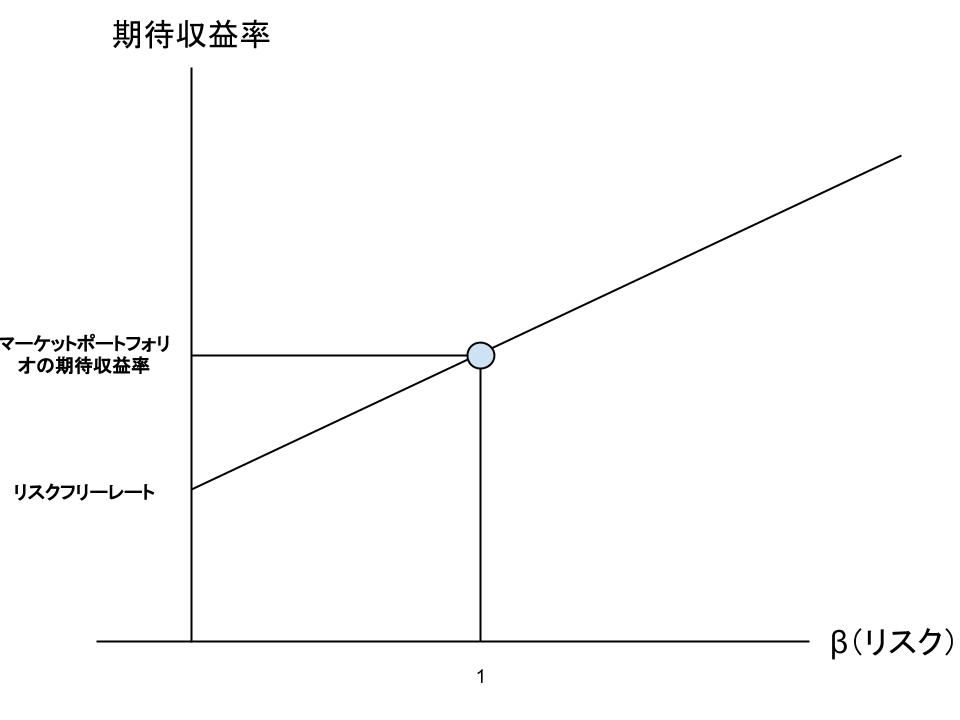
このように図示して考えてみると、どうやら式の「傾き」に誤りがあるようです。
Mさんは、現在の式の傾きである「β（ベータ）×マーケットポートフォリオの期待収益率」が間違っていると理解しました。
そこでMさんは傾きについて、もう一度考えてみました。
傾きは、βが1のときに期待収益率がマーケットポートフォリオと同じにならなければなりません。
そうすると、βが1のときにマーケットポートフォリオと同じとなる個別の株式の期待収益率は、「マーケットポートフォリオの期待収益率−リスクフリーレート」となります。
βが0の場合にすでにリスクフリーレートが加算されているためです。
そこでMさんは以下のような式を考えました。
期待収益率 ＝リスクフリーレート＋ β（ベータ）×（マーケットポートフォリオの期待収益率−リスクフリーレート）
これだとすっきりしそうな気がします。
そこでMさんは、この式でもう一度K社の期待収益率を計算してみました。
K社の期待収益率 ＝ 2＋1×（6−2） ＝ 6％
これだとマーケットポートフォリオの期待収益率と同じになります。
また、Mさんは確認のためにβが0.5の場合も考えてみることにしました。
βが0.5の場合の期待収益率 ＝ 2＋0.5×（6−2） ＝ 4％
すると今度はマーケットポートフォリオと比例していないことに気づきました。
マーケットポートフォリオと連動するとしたら、期待収益率は半分の3％になるはずです。
Mさんは悩んでしまい、Nさんにこのことを聞いてみました。
するとNさんはこう答えました。
「それで正解なんだよ。リスクフリーレートがある限り、期待収益率はリスクフリーレートに左右されることになるんだ。βが0.5の場合は期待収益率はリスクフリーレートとマーケットポートフォリオの中間の値である4になるし、βが2の場合は12ではなくリスクフリーレートを引いた10ということになる。常に期待収益率はリスクフリーレートの存在が加味されるということだよ。」
これでMさんは自分の手でCAPMの公式を導出できたのだということがわかりました。
そして少し自分が進歩できたのではという実感を持つことができました。
関連ページ
- 運転資金を即日調達する方法「ファクタリング」とは？【Q&A付き】
- ファイナンスとは
- 「儲け」とは
- 財務諸表とファイナンス その1
- 財務諸表とファイナンス その2
- キャッシュフローを理解する その1
- キャッシュフローを理解する その2
- キャッシュフローを理解する その3
- 埋没コストと機会費用
- 企業経営とキャッシュフロー概念 その1
- 企業経営とキャッシュフロー概念 その2
- 現在価値を理解する その1
- 現在価値を理解する その2
- 現在価値の計算
- 永続価値を理解する その1
- 永続価値を理解する その2
- リースファクター（年金現価係数） その1
- リースファクター（年金現価係数） その2
- リスクを理解する その1
- リスクを理解する その2
- リスクとポートフォリオ その1
- リスクとポートフォリオ その2
- ファイナンスのための統計学基礎
- リスクとリターン その1
- リスクとリターン その2
- リスクとリターン その3
- ポートフォリオの拡張と最適ポートフォリオ
- CAPM（Capital Asset Pricing Model）とは
- β（ベータ）を理解する
- CAPMの公式と解明 その1
- CAPMの公式と解明 その2
- ファンダメンタル価値理論と砂上の楼閣理論
- 効率的市場仮説とランダムウォーク
- 資本コスト（WACC）を理解する その1
- 資本コスト（WACC）を理解する その2
- 資本コスト算定の注意点
- 財務レバレッジとβ（ベータ） その1
- 財務レバレッジとβ（ベータ） その2
- 財務レバレッジとβ（ベータ） その3
- バリュエーションを理解する
- NPV（Net Present Value：正味現在価値）
- NPVによる投資評価 その1
- NPVによる投資評価 その2
- NPVの注意点
- APV（Adjusted Present Value：調整現在価値）
- NPVとAPVの関係
- IRR（Internal Rate of Return：内部収益率）
- EVA（Economic Value Added：経済的付加価値）
- MVA（Market Value Added：市場付加価値）
- 回収期間（Payback）法と会計上の収益率 その1
- 回収期間（Payback）法と会計上の収益率 その2
- PI（Profitability Index：収益性指標）
- 負債を活用した場合のNPV
- 企業価値を理解する
- 株価の理論値を理解する その1
- 株価の理論値を理解する その2
- 連結決算が企業価値に与える影響
- 経営の多角化が企業価値に与える影響
- M＆A（企業の合併・買収） その1
- M＆A（企業の合併・買収） その2
- 財務政策を理解する
- 最適資本構成とMM理論 その1
- 最適資本構成とMM理論 その2
- 利益還元政策を理解する その1
- 利益還元政策を理解する その2
- 株主に報いるには
- オプションを理解する その1
- オプションを理解する その2
- プレミアムの算定（二項過程モデル、ヘッジレシオ、プット・コール・パリティ） その1
- プレミアムの算定（二項過程モデル、ヘッジレシオ、プット・コール・パリティ） その2
- プレミアムの算定（二項過程モデル、ヘッジレシオ、プット・コール・パリティ） その3
- ブラック-ショールズの公式
- リアルオプションを理解する
- 負債コストとオプションの関係
- 「格付け」を理解する
- 経営戦略とファイナンス その1
- 経営戦略とファイナンス その2
- コーポレートガバナンス（企業統治）を理解する その1
- コーポレートガバナンス（企業統治）を理解する その2
- 資金調達方法（負債と自己資本） その1
- 資金調達方法（負債と自己資本） その2
- 資金調達方法（負債と自己資本） その3
- 資金計画を考える
- IR（インベスター・リレーションズ）とは
- 証券化とは