グラフの用法

トップページ＞経済学＞グラフの用法

今回はグラフの用法について説明していきます。

この文章を読むことで、グラフを用いる目的やグラフ解析で注意すべき問題について学ぶことができます。

グラフを用いる目的とは

経済学上必要になる概念の多くは数値化できるものです。

その数値を視覚化するグラフは大きく2つの役割持っています。

1.わかりやすく説明する

2.データ分析を容易にする

以下では、グラフの基本的な考え方からどのように用いるかを見ていくことで、この2つの役割について考えていきます。

単一変数のグラフ

単一変数のグラフは、得られるデータがたった1つの場合のグラフです。

数字の羅列を視覚化することで、言葉では説明しにくい内容を一見してわかるようにする役割を持ちます。

以下で具体的に見ていきましょう。

【例題1】

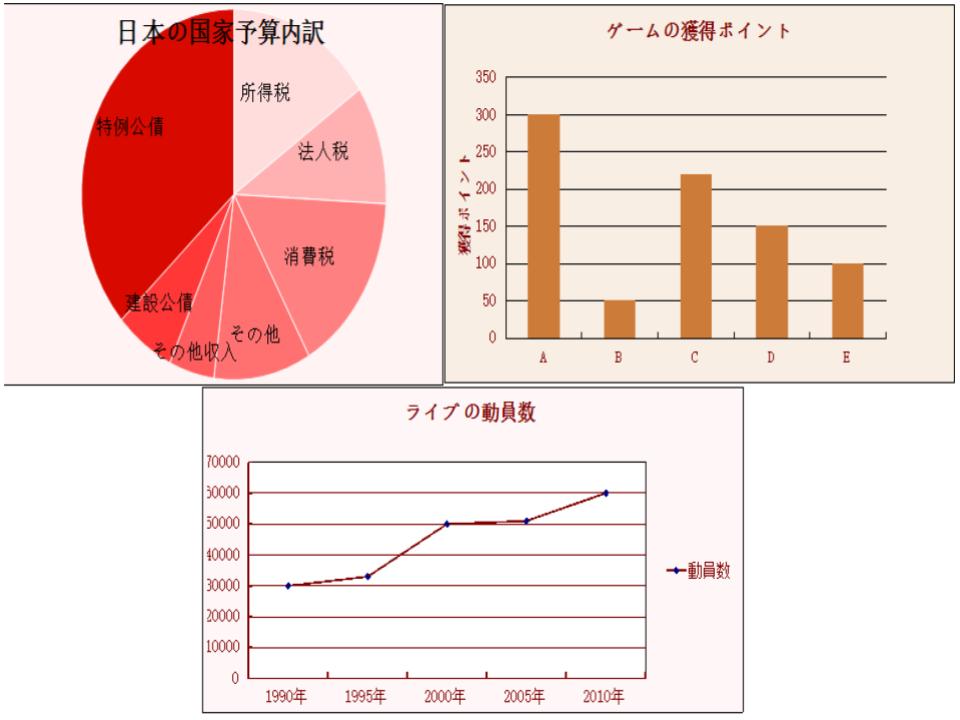
グラフの用法1

＜解説＞
これらは極めて一般的なグラフです。

左上は円グラフ。国家予算の歳入出の内訳などを知る際に非常に重宝するグラフです。

どの項目がどれくらいの割合を占めているかが一目で把握できるため、例えば日本の歳入のうち43％が借金でまかなわれているという事実をよりドラマチックに説明できます。

右上の棒グラフは、グラフの高さによって数値の違いが比較しやすいという特長があります。

ゲームでの獲得ポイントの比較や、政治家の支持率の比較などには最適なグラフです。

また、時系列に従って数値の推移を追うのであれば折れ線グラフが最も優れているでしょう。

1990年30000人、1995年33000人、2000年50000人…などと数字で羅列されるよりも、どの時期にどれだけ増えているのかが、一目瞭然なはずです。

時系列データに関しては変数が「時間」と「動員人数」で分かれているため、二変数のようにも見えますが、時間の流れは一定であるため、単一変数のグラフとして考えます。

単一変数のグラフができないこととグラフの罠

単一変数の場合、データ解析についての有用性は劣っていると言わざるを得ません。

なぜなら、データ分析の簡便化という意味では、データの数が1つしかないために得られる情報が少ないからです。

また、グラフにすると視覚的にわかりやすくなるため、使い方や見方によっては情報をミスリードしてしまう危険性があります。

例えば、折れ線グラフの横軸の数字を小さくして、0だった時点からの伸びを大きなものと錯覚させたりすることが可能なのです。

わかりやすいだけにそのようなリスクがあることも知っておきましょう。

二変数のグラフ

単一変数のグラフではどうしてもデータの数の面で、データ分析を容易にする効用は低くならざるを得ませんでした。

それに対して、二変数のグラフを使えば変数間の関係性を一つのグラフの中で観察できるため、データ分析の簡便性は格段に上昇します。

では、こちらも具体的に見ていきましょう。

【例題1】

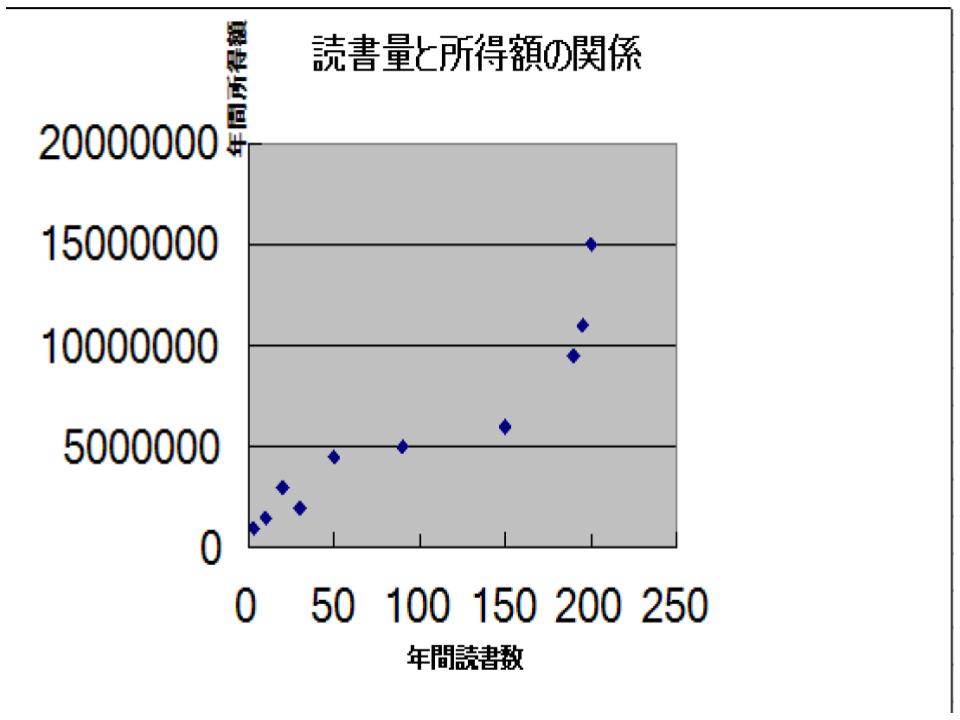
グラフの用法2

＜解説＞
このグラフは散布図と呼ばれるものです。

縦軸に「年間読書数」をとり、横軸に「年間所得額」をとった例のようなグラフがあったとします。

このグラフによれば、「本を読んでいる人ほどお金持ちである」ということができるでしょう。

他にも「理科の点数」と「数学の点数」をグラフ化すれば「数学ができる人は理科も得意なのか」という疑問に答えを出すこともできます。

あるいは、「1週間に自炊する回数」と「最高血圧」でグラフを作れば、「自炊する回数が多いほど血圧が低い」といった分析も可能になるかもしれません。

二変数間の相関関係を明らかにするために、散布図は最適なのです。

そこに因果関係はあるのか

しかし、このグラフでもミスリードの可能性は排除できません。

前掲のグラフで言えば、「本をたくさん読んでいる人にはお金持ちが多い」という分析はできても、それは「本を読めばお金持ちになれる」という因果関係の証明にはなりません。

お金持ちになるには読書量以外の要素も大きく関係しているからです。

ダイエット食品の広告などに「食品の購入量」と「3か月間で減った体重」をグラフに示して「この食品をたくさん買っている人ほど痩せています！」と書かれてあったとします。

それを安直に「その食品を食べれば痩せる」という意味だとは解釈してはいけないのです。

曲線が「シフト」する

二変数のグラフにおいて、どちらの軸にも含まれていない変数が変化するとき、曲線はいずれかの方向にシフトします。

グラフの形を左右するこの原因となる要素を「変数」と呼びますが、前述のような二変数のグラフで全てを示すことのできるケースは少ないと言っていいでしょう。

なぜなら、経済における出来事のみならず、日常のあらゆる出来事は複数の原因によって結果を左右されるからです。

自動車を購入する際に数多くのメーカーの中からトヨタの車を選ぶ理由は「車が欲しかったから」という一つの理由ではないはずで、同様にある日の夕食をハンバーグ定食にした理由も、また一つではないはずです。

そこには様々な変数が関与しており、そのうちの一つが変化すれば、自ずと結果にも影響を及ぼすのです。それをグラフに反映させたとき、シフトするのです。

どういうことか、具体的に例を見てみましょう。

【例題3】
Aさんは大のビール党で、お酒を飲むのならビール、炭酸を飲むのならビールというくらいビールが大好きです。

そんなAさんのビールの年間購入本数を、ビール1缶の価格の変動と関連させたグラフが下図のグラフ1です。

ビールの値段が80円の時は360本、95円の時は288本、108円の時は264本、136円になると192本でした。

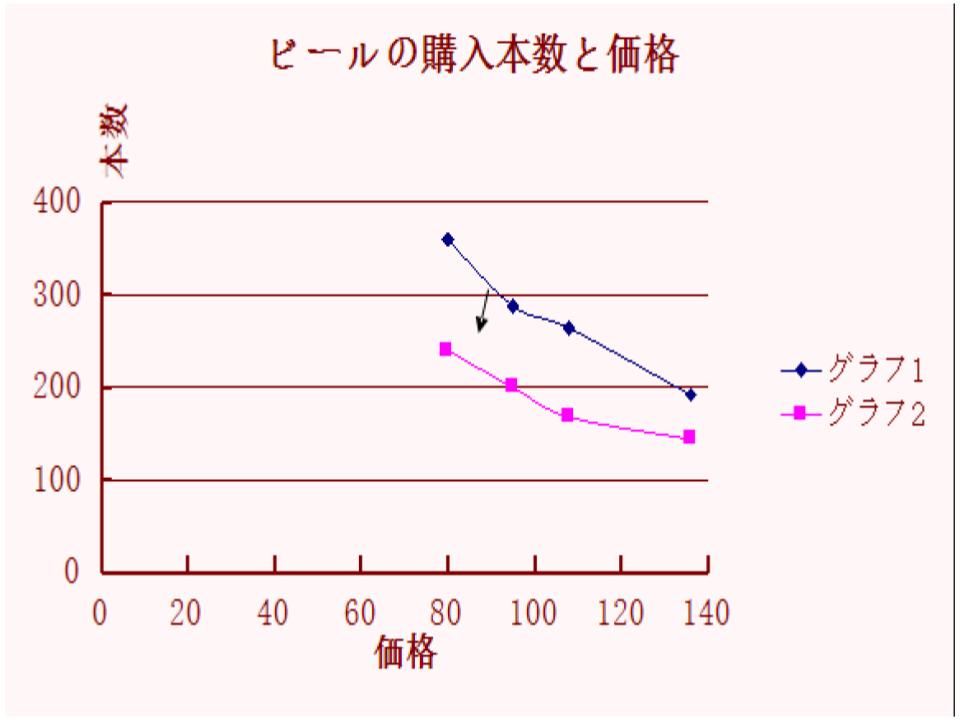
グラフの用法3

＜解説＞
この時考慮すべきは、この図において年間購入本数と価格以外の全ての変数は固定されているという点です。

でなければ、このデータは何の信ぴょう性もありません。

例えば、Aさんの年間所得という変数を考えるとき、仮に80円の時の所得が200万円で95円の時の所得が150万円であった場合です。

95円の時にも所得が200万円であれば、購入本数はまるで違う数字になっている可能性が十分に考えられるからです。

グラフ内の二軸にない変数が変化したとき、図のように別のグラフに表されます。

グラフ1の時のAさんの所得を200万円とします。

所得が150万円で、かつ1缶の価格が95円の時のAさんの購入本数が200本であった場合のグラフはグラフ2です。

グラフが下にシフトしたのがわかると思います。

変数は無数にある

しかし、このように本数、価格、所得だけを考慮しても、まだまだ変数を網羅できたわけではありません。

例えば、代替品となり得るチューハイの価格や、健康上の問題になりかねない血圧の数値などは十分に年間購入本数に影響しうる変数です。

これらが変化した場合にもグラフはシフトしなくてはなりません。

傾きは何を表すか

次に考えるのはグラフの傾きについてです。

傾きはxの値の変化に、どれだけyの値が反応するのか、あるいはyの変化にxがどれだけ反応するのかを示しています。

前述のAさんのグラフを参考に考えましょう。

グラフ1のうち（95.288）、（108.264）の2つの点の時の傾きは比較的緩やかです。

この価格帯の時、Aさんの購入本数はあまり変わっていません（13円の値上げに対して24本の減少）。

対して（80.360）⇒（95.288）の間の傾きは先ほどのものと比べると急です。

つまり、80円から95円に15円上がった時の方が、Aさんはより多く購買意欲を削がれたのです（72本の減少）。

傾きは次の式で求めることが可能です。

傾き＝ △y / △x　　

△（デルタ）は変化量を示しています。

先ほどの（95.288）、（108.264）のときの傾きは次のような式で求められます。

傾き＝(288-264) / (95-108)＝−24 / 13

傾きが水平の時・垂直の時

グラフには傾きが水平の時や垂直の時もあります。この場合は一体どのような状況を示しているのでしょうか？

Aさんのグラフが仮に水平だった場合、いくら価格xが変動しても購入本数yは変動しないことになります。

つまり「いくらであってもビールを飲む量は変わらない」のです。

逆に垂直の時は、ビールがずっと95円を維持していても、Aさんはビールの購入本数を変化させるという状況になります。

この場合、Aさんの購入するビールの本数には限りがないということも意味します。

曲線のシフトと傾き

曲線はx軸とy軸にとられていない以外の要素（＝変数）が変化する場合、左右上下の方向いずれかにシフトします。

この変数は無数にあるため、注意が必要です。

また、グラフの傾きは一方の変数が一方の変数にもたらす影響力を示します。

傾きが急であればxの値がyの値に及ぼす影響は大きく、緩やかであれば影響は小さいと言えます。

この逆もまた然りです。

傾きを見れば、意思決定に大きな影響を及ぼす値の見当を付けることもできます。

グラフ解析で注意すべき2つの問題

ここまでみてきたように、グラフを見ることでデータの内容をわかりやすくしたり、複数のデータの相関関係を考えることが可能になります。

しかし、このデータの相関関係を考える場合に、どうしても無視できない大きな問題が二つある点を忘れてはいけません。

1.捨象された変数

2.逆因果関係

捨象された変数とは、例えば二変数のグラフにおいては、グラフ上で考慮されているのはxとyの二つの値だけです。

グラフにおける相関関係を考えるうえで、この2つ以外の数字は完全に無視（捨象）されています。

ここには「二変数以外の数値は全て固定されている」という大前提が存在していますが、これが可能にあるのはあくまで仮定の世界だけで、現実の世界ではこの前提を維持するのは非常に難しくなります。

他の数値が固定されているという事実を忘れてしまうと、グラフの解析にあたって大きな勘違いが起き得ます。

x以外の第三、第四の変数がyの値に大きな影響をもたらしているのにもかかわらず、一見すればxの増減に従ってyが増減している風に見えるため、xとyの間の因果関係を誤認してしまうのです。

しかし、仮に最も適切な二変数を選別できたとして、問題はまだあります。

というのも、xの変化が原因でyが変化しているのにもかかわらず、yの変化が原因でxが変化していると勘違いしてしまう可能性を排除できないのです。

これらについてどのような状況が考えられるか、具体的に見ていきましょう。

【例題4】
エナジードリンクの消費量が多い人ほど過労が原因で死亡することが多いという統計結果が出ました。

これを受けて週刊誌は「エナジードリンクを飲むと過労死する！？消費者に公開されていない猛毒レシピ！」などと銘打って数多くのバッシング記事を発表し、政府はと言えばエナジードリンクへの特別消費税を施行し、タバコと同じくらいの税金をかけると閣議決定します。

さて、ここではどんな因果関係の勘違いが起こっているでしょうか？

＜解説＞
まず考えるべきは、「どんな変数が捨象されているか」です。

過労死の最も大きな原因は「働きすぎ」です。捨象されている変数は「労働時間」です。

過労死の直接の死因は心疾患や脳疾患、自殺などですからそれらによる死亡者数も変数に組み込む必要があるかもしれません。

夜中も働き続けるためにはエナジードリンクがより多く必要になります。であるならば、労働時間が延びればエナジードリンクの消費量も自ずと増加します。

この場合、本来は労働時間が原因なのにもかかわらずそれを捨象してしまっているために、「エナジードリンクの飲む人ほど過労死しやすい」という誤った観測がされてしまったのです。

マスコミは働かせすぎの企業を批判すべきで、政府は労働基準法の順守のための罰則規定の強化をすべきなのです。

【例題5】
肥満度の高い人が多く住む町ほど半径1?圏内の飲食店が多くあるということがわかりました。

これを受けて日本肥満撲滅委員会は「外食産業があるから肥満が増えるんだ。政府には即刻飲食店の出店規制を設けるよう要求する！」という声明を出しました。

これを受けて外食産業推進委員会は、「日本肥満撲滅委員会の言うことは全く逆だ。私たちは市場原理に従って需要のある土地に出店しているだけだ。私たちが出店した後肥満度の高い人たちが移住してきたんだ」と主張します。

さて、どちらの主張が正しいのでしょうか？

＜解説＞
この主張の是非を判断するには、冒頭の統計だけでは情報不足です。

例えば、当該地域に10年以上住んでいる人たちの直近10年間の体重変化と外食に行く回数、そして当該期間の半径1?圏内の飲食店の増減などを調べれば、明らかになるかもしれません。

しかし、それでも決定的な変数は見つからない可能性もあります。

元来、因果関係の順番を明確にするための方程式は存在せず、蓋然性（確からしさ）の高い可能性を使って判断していくしかないのです。

例えば、スマートフォンの利用者の増加とスマートフォン依存症の増加を比較した際に、「スマートフォン依存症の人が増えたからスマートフォン利用者が増えたんだ」と結論付ける人はいないはずです。

何が原因で何が結果なのかを判断する際には、グラフよりも論理的な手続きの方が重要です。

まとめ

＜グラフの利点＞

わかりやすく説明する。

データ分析を容易にする。

＜グラフの落とし穴＞

・捨象された変数

・逆因果関係

経営を学ぶ-経営学･MBA･起業･ネットビジネス･リアルビジネスなど